На этом шаге мы закончим изучение этого вопроса.

Код

В примере 4.1 показано, как создать простую модель линейной регрессии с помощью одной строки кода (возможно, вам нужно будет сначала установить библиотеку scikit-learn путем выполнения в командной оболочке команды pip install sklearn).

Пример 4.1. Простая модель линейной регрессии

from sklearn.linear_model import LinearRegression
import numpy as np

## Данные (курс акций Apple)
apple = np.array([155, 156, 157])
n = len(apple)

## Однострочник
model = LinearRegression().fit(np.arange(n).reshape((n, 1)), apple)

## Результат
print(model.predict([[3], [4]]))

Архив с файлом можно взять здесь.

Можете ли вы уже угадать, какие результаты вернет этот фрагмент кода?

Принцип работы

В этом однострочнике используется две библиотеки Python: NumPy и scikit-learn. Первая из них - фактически стандартная библиотека для численных вычислений (например, операций с матрицами). Вторая - самая обширная библиотека для машинного обучения, включающая реализации сотен алгоритмов и методик машинного обучения.

Возможно, вы спросите: "Почему вы используете библиотеки в однострочнике Python? Не жульничество ли это?" Хороший вопрос, ответ на который - да. Любая программа на языке Python - с библиотеками или без - использует высокоуровневую функциональность, в основе которой лежат низкоуровневые операции. Нет смысла изобретать колесо, когда можно повторно задействовать уже существующую базу кода (то есть встать на плечи гигантов). Начинающие разработчики часто стремятся реализовать все самостоятельно, что снижает их производительность. В этом изложении мы хотели бы не игнорировать широкий спектр функциональности, реализованной лучшими разработчиками и первопроходцами Python, а использовать во всей полноте. Разработка, оптимизация и шлифовка каждой из этих библиотек заняла у высококвалифицированных разработчиков многие годы.

Рассмотрим пример 4.1 шаг за шагом. Во-первых, мы создали простой набор данных из трех значений и сохранили его длину в отдельной переменной n ради сокращения кода. Наши данные состоят из трех курсов акций Apple за три последовательных дня. Этот набор данных хранится в переменной apple в виде одномерного массива NumPy.

Во-вторых, мы создали модель с помощью вызова LinearRegression(). Но какие значения параметров будут у этой модели? Чтобы их найти, мы обучаем модель с помощью вызова функции fit(). Она принимает два аргумента: входные признаки обучающих данных и желаемые выходные сигналы для этих входных сигналов. Роль желаемых выходных сигналов играют настоящие курсы акций Apple. Входные же признаки необходимо передать fit() в виде массива в следующем формате:

  [<обучающие_данные_1>,
   <обучающие_данные_2>,
   .   .   .   .
   <обучающие_данные_n>]

где каждое значение обучающих данных представляет собой последовательность значений признаков:

  <обучающие_данные> = [признак_1, признак_2, ..., признак_k]

В нашем случае входной сигнал состоит лишь из одного признака x (текущий день). Более того, предсказание также состоит лишь из одного значения у (текущий курс акций). Чтобы изменить форму входного массива на нужную, необходимо привести его к виду следующей матрицы, выглядящей странновато:

  [[0],
   [1],
   [2]]

Матрица из одного столбца называется вектором-столбцом. Для создания последовательности возрастающих значений x мы применим метод np.arange(), а затем воспользуемся reshape((n, 1)) для преобразования одномерного массива NumPy в двумерный, содержащий один столбец и n строк. Обратите внимание, что scikit-learn допускает одномерный массив в качестве выходного сигнала (иначе нам бы пришлось изменить и форму массива данных apple).

Получив обучающие данные и желаемые выходные сигналы, функция fit() производит минимизацию погрешности: находит такие параметры модели (то есть прямую), что разность между предсказанными моделью значениями и желаемыми выходными сигналами минимальна.

Когда функция fit() сочтет, что модель доведена до ума, она возвращает модель, пригодную для предсказания двух новых значений курсов акций с помощью функции predict(). Требования к входным данным у функции predict() те же, что и у fit(), поэтому для их удовлетворения мы передаем матрицу из одного столбца с нашими двумя новыми значениями, для которых требуются предсказания:

  print(model.predict([[3],[4]]))

А поскольку минимизированная погрешность равна нулю, то должны получиться идеально линейные результаты: 158 и 159, которые прекрасно соответствуют прямой, построенной на рисунке 3 предыдущего шага. Но зачастую найти столь прекрасно подходящую линейную модель не получается. Например, если запустить ту же функцию для курсов акций [157, 156, 159] и построить соответствующий график, то получится прямая, изображенная на рисунке 1.

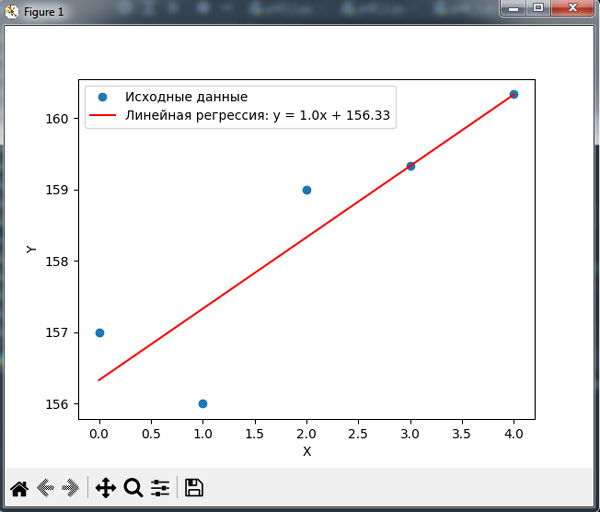
Рис.1. Неидеально подогнанная модель линейной регрессии

В этом случае функция fit() находит прямую, минимизирующую квадрат погрешности между обучающими данными и предсказаниями, как и упоминалось ранее.

Резюмируем: линейная регрессия - методика машинного обучения, при которой модель усваивает коэффициенты как параметры модели. Полученная в итоге линейная модель (например, прямая на плоскости) может непосредственно выполнять предсказания на основе новых входных данных. Задача предсказания числовых значений по заданным числовым входным значениям относится к классу задач регрессии. Из следующего шага вы узнаете еще об одной важной сфере машинного обучения классификации.

На следующем шаге мы рассмотрим логистическую регрессию.

Предыдущий шаг Содержание Следующий шаг