На этом шаге мы приведем теоретическое описание этой регрессии.
Логистическая регрессия часто применяется для задач классификации, в которых предсказывается, относится ли конкретный пример данных к конкретной
категории (классу). Эта постановка отличается от задач регрессии, в которых по заданному примеру данных необходимо предсказать числовое значение,
относящееся к непрерывному диапазону. Пример задачи классификации: разбиение пользователей Twitter на мужчин и женщин по заданным различным
входным признакам, например частоте отправки ими твитов или количеству ответов на твиты. Модель логистической регрессии относится к наиболее
основополагающим моделям машинного обучения. Многие из понятий, с которыми вы познакомитесь на этом шаге, станут основой для более продвинутых
методик машинного обучения.
Общее описание
Чтобы познакомиться с логистической регрессией, кратко рассмотрим, как работает линейная регрессия: по входным данным вычисляется прямая, лучше всего подходящая для этих обучающих данных, и предсказывается выходной сигнал для входного сигнала x. В целом линейная регрессия прекрасно подходит для предсказания непрерывного выходного сигнала, величина которого может принимать бесконечное количество значений. Предсказанные ранее курсы акций, например, могут теоретически принимать любые положительные значения.
Но что, если выходной сигнал не непрерывный, а категориальный, то есть принадлежит к ограниченному количеству групп или категорий? Например, пусть мы
хотим предсказать правдоподобие рака легких, исходя из количества выкуренных пациентом сигарет. У каждого пациента либо есть рак
легких, либо нет. В отличие от курсов акций, возможных исходов только два. Предсказание правдоподобия категориальных исходов - основная причина
использования логистической регрессии.
Сигма-функция
Если линейная регрессия подгоняет к обучающим данным прямую, то логистическая регрессия подгоняет к ним S-образную кривую - так называемую сигма-функцию (the sigmoid function). S-образная кривая упрощает выбор из двух альтернатив (например, да/нет). Для большинства входных сигналов сигма-функция возвращает значение, очень близкое либо к 0 (одна категория), либо к 1 (другая категория). Неоднозначный результат относительно маловероятен. Отметим, что для конкретных входных значений могут быть сгенерированы и равные 0.5 вероятности, но форма кривой специально выбрана таким образом, чтобы минимизировать возможность этого на практике (для большинства значений горизонтальной оси координат величина вероятности очень близка либо к нулю, либо к единице). На рисунке 1 приведена кривая логистической регрессии для прогноза рака легких.
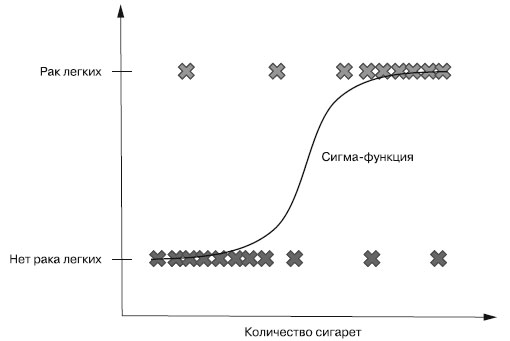
Рис.1. Кривая логистической регрессии для предсказания рака по количеству выкуриваемых сигарет
Логистическую регрессию можно применять и для полиномиальной классификации (multinomial classification), при которой данные классифицируются
более чем по двум классам. Для этого используется обобщение сигма-функции - так называемая многомерная логистическая функция (softmax function),
возвращающая кортеж вероятностей, по одной для каждого класса. Сигма-функция же преобразует входной (-ые) признак (-и) в одно значение вероятности.
Впрочем, ради простоты и удобочитаемости мы сосредоточим свое внимание на биномиальной классификации (binomial classification).
Сигма-функция на рисунке 1 аппроксимирует вероятность наличия у пациента рака легких в зависимости от количества выкуриваемых им сигарет. Исходя из этой вероятности, можно четко определить при наличии одной только информации о количестве выкуриваемых пациентом сигарет, есть ли у пациента рак легких.
Взгляните на предсказание на рисунке 2, на котором представлены два новых пациента (изображены светло-серым цветом внизу графика).
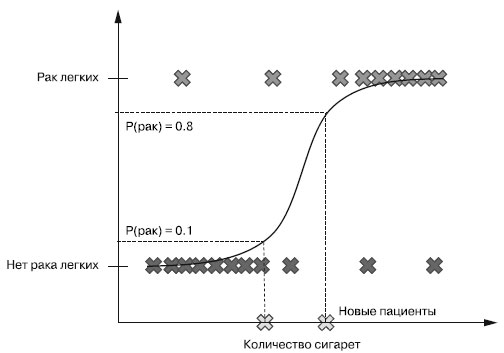
Рис.2. Оценка вероятностей исходов с помощью логистической регрессии
Нам ничего о них не известно, кроме количества выкуриваемых ими сигарет. Мы обучаем модель логистической регрессии (сигма-функцию), возвращающую
вероятность для любого нового входного значения х. Если возвращающая сигма-функцией вероятность выше 50%, то модель выдает предсказание
онкопозитивный, в противном случае - онконегативный.
Поиск модели максимального правдоподобия
Основной вопрос метода логистической регрессии - как выбрать правильную сигма-функцию, лучше всего соответствующую обучающим данным. Для ответа на него используется такое понятие, как правдоподобие (likelihood) модели: возвращаемая моделью вероятность для наблюдаемых обучающих данных. Желательно выбрать модель с максимальным правдоподобием. Идея в том, чтобы эта модель лучше всего аппроксимировала реальный процесс, в результате которого были сгенерированы обучающие данные.
В целях вычисления правдоподобия заданной модели для заданного набора обучающих данных вычисляется правдоподобие для каждой из обучающих точек данных, и в результате их перемножения получается общее правдоподобие для всего набора обучающих данных. Как же вычислить правдоподобие отдельной обучающей точки данных? Достаточно просто применить к ней сигма-функцию модели, чтобы получить вероятность для указанной точки данных при использовании этой модели. Чтобы выбрать модель максимального правдоподобия для всех точек данных, необходимо повторить это вычисление правдоподобия для различных сигма-функций (выбираемых с небольшим сдвигом), как показано на рисунке 3.
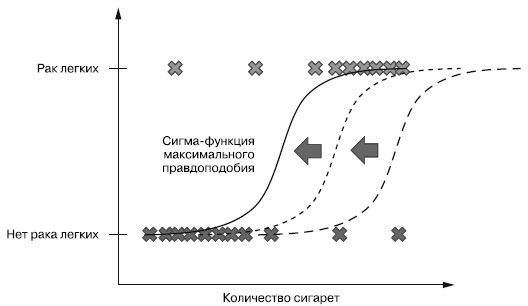
Рис.3. Поиск максимального правдоподобия путем проверки различных сигма-функций
В предыдущем абзаце мы говорили, как определить сигма-функцию (модель) максимального правдоподобия, которая лучше всего описывает данные, поэтому можно ее использовать для предсказания новых точек данных.
С теоретической частью покончено. Теперь посмотрим, как можно реализовать логистическую регрессию в виде однострочника Python.
На следующем шаге мы закончим изучение этого вопроса.
