На этом шаге мы рассмотрим суть алгоритма кластеризации методом k-средних.
Если и есть алгоритм кластеризации, который пригодится и обычному специалисту в области компьютерных наук, и исследователю данных, и специалисту по
машинному обучению, то это алгоритм кластеризации методом k-средних (k-means algorithm). На текущем шаге мы обсудим общую идею,
а также рассмотрим, когда и как использовать его с помощью всего одной строки кода на Python.
Общее описание
В предыдущем примере мы рассматривали обучение с учителем, при котором обучающие данные маркированы, то есть известны выходные значения для всех входных признаков в обучающих данных. Но на практике так бывает далеко не всегда. Зачастую исследователи сталкиваются с немаркированными данными, особенно в приложениях аналитической обработки данных, когда непонятно, какой выходной сигнал будет "оптимальным". В подобном случае предсказать что-либо невозможно (поскольку отсутствует эталонный выходной сигнал), но все равно можно извлечь из этих немаркированных наборов данных немало полезной информации (например, найти кластеры схожих немаркированных данных). Модели, работающие с немаркированными данными, относятся к категории моделей машинного обучения без учителя (unsupervised learning).
В качестве примера представьте, что работаете над стартапом, обслуживающим различную целевую аудиторию, разного возраста и с разным доходом. Ваш начальник просит найти определенное количество персон, лучше всего соответствующих вашей целевой аудитории. Для выявления усредненных персон заказчиков в вашей компании можно воспользоваться методами кластеризации. На рисунке 1 приведен пример.
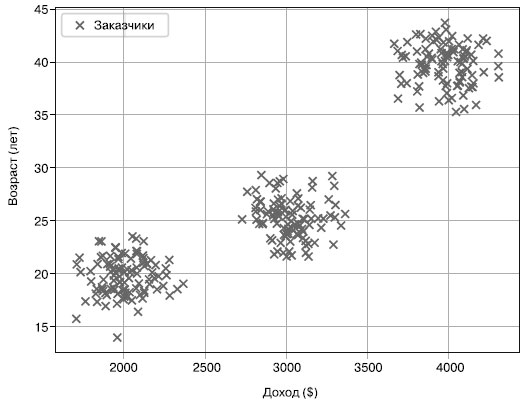
Рис.1. Наблюдаемые данные о заказчиках в двумерном пространстве
На данном рисунке можно с легкостью выделить три типа персон различного уровня доходов и возраста. Но как сделать это алгоритмически? Тут-то и вступают в дело алгоритмы кластеризации наподобие очень популярного алгоритма кластеризации методом k-средних. При заданном наборе данных и целом числе k алгоритм кластеризации методом k-средних находит k кластеров данных, таких что расстояние между центром кластера (так называемым центроидом) и данными в этом кластере минимально. Другими словами, путем выполнения алгоритма кластеризации методом k-средних можно найти различные персоны в ваших наборах данных, как показано на рисунке 2.
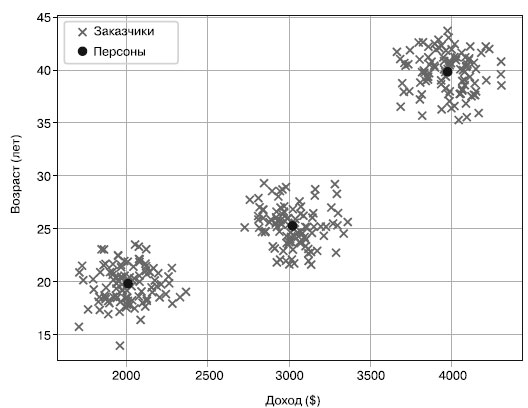
Рис.2. Данные о заказчиках с персонами заказчиков (центроидами кластеров) в двумерном пространстве
Центры кластеров (черные точки) отмечают кластеризованные данные о заказчиках. Каждый центр кластера можно считать одной персоной заказчика. Таким образом, у нас есть три персоны: 20-летний заказчик с доходом в 2000 долларов, 25-летний с доходом в 3000 долларов и 40-летний с доходом в 4000 долларов. Замечательно то, что алгоритм кластеризации методом k-средних находит эти центры кластеров даже в многомерном пространстве (в котором найти их визуально для человека было бы непросто).
Алгоритм кластеризации методом k-средних требует на входе "количество центров кластеров k". В данном случае мы смотрим на данные и каким-то чудесным образом выбираем k = 3. Более продвинутые алгоритмы могут находить количество центров кластеров автоматически.
Как же работает алгоритм кластеризации методом k-средних? По существу, он сводится к следующей процедуре:
Задать случайные начальные значения для центров кластеров (центроидов)
Повторять до достижения сходимости
Распределить все точки данных по ближайшим к ним центрам кластеров
Повторить вычисление всех центров кластеров, приписанных к ним всех точек данных
как центроидов
Все это приводит к многочисленным итерациям цикла: сначала данные приписываются к k центрам кластеров, а затем каждый центр кластера пересчитывается как центроид приписанных к нему данных.
Реализуем его!
Рассмотрим следующую задачу: найти в данном наборе двумерных данных о зарплатах (отработанные часы, заработанные деньги) два кластера сотрудников, работающих одинаковое количество часов и зарабатывающих примерно одинаковые деньги.
На следующем шаге мы закончим изучение этого вопроса.
