На этом шаге мы закончим изучение этого вопроса.
Код
Как реализовать все это в одной строке кода? К счастью, библиотека scikit-learn Python включает готовую эффективную реализацию алгоритма кластеризации методом k-средних. Пример 4.3 демонстрирует фрагмент кода с однострочником, выполняющим кластеризацию методом k-средних.
Пример 4.3. Кластеризация методом k-средних в одной строке
## Зависимости from sklearn.cluster import KMeans import numpy as np ## Данные (Отработано (ч) / Зарплата ($)) X = np.array([[35, 7000], [45, 6900], [70, 7100], [20, 2000], [25, 2200], [15, 1800]]) ## Однострочник kmeans = KMeans(n_clusters=2).fit(X) ## Результат cc = kmeans.cluster_centers_ print(cc)
Каковы же будут результаты выполнения этого фрагмента кода? Попробуйте догадаться, даже если не понимаете некоторых нюансов синтаксиса. Это
поможет вам осознать пробелы в своих знаниях и намного лучше подготовиться к восприятию алгоритма.
Принцип работы
В первых строках мы импортируем модуль KMeans из пакета sklearn.cluster. Этот модуль отвечает за саму кластеризацию. Необходимо также импортировать библиотеку NumPy, поскольку модуль KMeans использует в своей работе ее массивы.
Наши данные - двумерные, они соотносят количество отработанных часов с зарплатой некоторых работников. На рисунке 1 показаны шесть точек данных из этого набора данных.
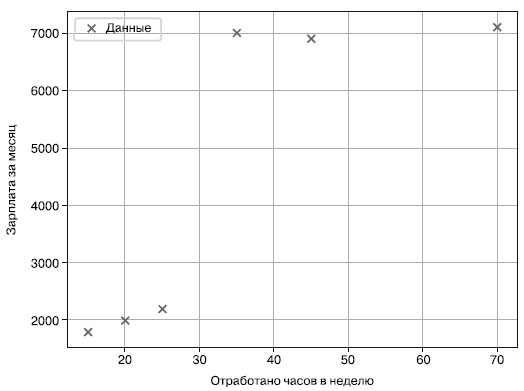
Рис.1. Данные по зарплатам сотрудников
Задача - найти два центра кластеров, лучше всего удовлетворяющих этим данным:
## Однострочник
kmeans = KMeans(n_clusters=2).fit(X)
В этом однострочнике создается новый объект KMeans, который отвечает за выполнение алгоритма. При создании объекта KMeans описывается количество центров кластеров с помощью аргумента функции n_clusters. А затем мы просто вызываем метод экземпляра fit(X) для выполнения алгоритма кластеризации методом k-средних на входных данных X. Теперь все результаты содержатся в объекте KMeans. Осталось только извлечь эти результаты из его атрибутов:
cc = kmeans.cluster_centers_
print(cc)
Обратите внимание, что по соглашению в пакете sklearn в некоторых названиях атрибутов в конце указывается подчеркивание (например, cluster_ centers_), означающее, что эти атрибуты были созданы динамически на этапе обучения (в ходе вызова функции fit()). До этого их не существовало. Для Python такое соглашение не является стандартным (к подчеркиванию в конце названий прибегают обычно лишь во избежание конфликтов названий с ключевыми словами Python - например, переменная list_ вместо list). Однако когда вы привыкнете, то почувствуете удобство согласованного использования атрибутов в пакете sklearn. Какие же будут центры кластеров и вообще результат работы данного фрагмента кода? Взгляните на рисунок 2.
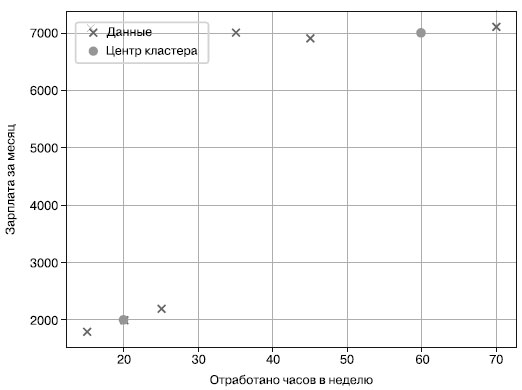
Рис.2. Данные по зарплатам сотрудников с центрами кластеров в двумерном пространстве
На рисунке видны два центра кластеров: (20, 2000) и (50, 7000). Это также результат нашего однострочника Python. Эти кластеры соответствуют двум персонам сотрудников: первый работает 20 часов в неделю и зарабатывает 2000 долларов в месяц, а второй работает 50 часов в неделю и зарабатывает 7000 долларов в месяц. Эти два типа персон неплохо удовлетворяют нашим данным. Следовательно, результат выполнения нашего однострочного фрагмента кода выглядит так:
## Результат cc = kmeans.cluster_centers print(cc) # [[ 50. 7000.] # [ 20. 2000.]]
Резюмируя: в двух последних шагах вы познакомились с важным подвидом машинного обучения без учителя: кластеризацией. Алгоритм кластеризации методом k-средних - простой, эффективный и популярный способ выделения k кластеров из многомерных данных. "Под капотом" алгоритм в цикле пересчитывает центры кластеров и перераспределяет все точки данных по ближайшим к ним центрам кластеров, пока не будут найдены оптимальные кластеры. Однако кластеры не всегда идеально подходят для поиска схожих элементов данных. Многие наборы данных не проявляют кластерной организации, но информацию о расстоянии все равно хотелось бы использовать для машинного обучения и предсказания. Не будем покидать многомерное пространство и рассмотрим еще один способ задействовать (евклидово) расстояние между значениями данных: алгоритм k-ближайших соседей.
На следующем шаге мы рассмотрим метод k-ближайших соседей в одной строке кода.
