На этом шаге мы закончим изучение этого вопроса.
Код
Посмотрим, как можно использовать KNN на языке Python - в одной строке кода (пример 4.4).
Пример 4.4. Выполнение алгоритма KNN с помощью одной строки кода на Python
## Зависимости from sklearn.neighbors import KNeighborsRegressor import numpy as np ## Данные (площадь дома (в квадратных метрах) / цена дома ($)) X = np.array([[35, 30000], [45, 45000], [40, 50000], [35, 35000], [25, 32500], [40, 40000]]) ## Однострочник KNN = KNeighborsRegressor(n_neighbors=3).fit(X[:, 0].reshape(-1, 1), X[:, 1]) ## Результат res = KNN.predict([[30]]) print(res)
Каковы же будут результаты выполнения этого фрагмента кода?
Принцип работы
Чтобы наглядно представить результат, построим график данных по ценам на жилье (рисунок 1).

Рис.1. Данные по ценам на жилье
Видите общую тенденцию? Можно предположить, что с ростом площади дома его рыночная стоимость также будет линейно расти. Вдвое больше квадратных метров - вдвое больше цена.
В коде (см. пример 4.4) клиент запрашивает предсказание цены для дома площадью 30 квадратных метров. Что же предскажет KNN при k = 3 (то есть 3NN)? Взгляните на рисунок 2.
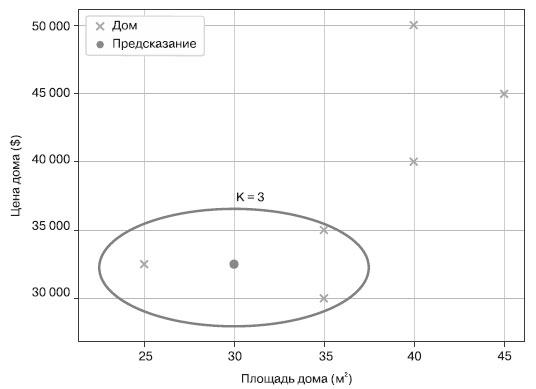
Рис.2. Данные о стоимости домов в двумерном пространстве с предсказанием цены дома для новой точки данных (площадь дома равна 30 м2) с помощью алгоритма KNN
Красота, правда? Алгоритм KNN находит три ближайших по площади дома и возвращает предсказанную стоимость дома как среднее k = 3 ближайших соседей. Таким образом, в результате получается 32 500 долларов.
Если вам не вполне понятны преобразования данных в этом однострочнике, то вкратце поясним их:
KNN = KNeighborsRegressor(n_neighbors=3).fit(X[:, 0].reshape(-1, 1), X[:, 1])
Прежде всего мы создаем новую модель машинного обучения - KNeighborsRegressor. Если нужно использовать KNN для классификации, то следует применить KNeighborsClassifier.
Далее мы обучаем модель с помощью функции fit() с двумя параметрами, первый из которых определяет входной сигнал (размер дома), а второй - выходной сигнал (стоимость дома). Оба параметра должны представлять собой массивоподобные структуры данных. Например, если нужно передать значение 30 в качестве входных данных, то следует передать его в виде [30]. Дело в том, что входные данные могут быть многомерными, а не только одномерными. Поэтому мы меняем форму входного сигнала:
print(X[:,0]) # [35 45 40 35 25 40]" print(X[:,0].reshape(-1,1)) # [[35] # [45] # [40] # [35] # [25] # [40]]
Обратите внимание, что при использовании этого одномерного массива NumPy в качестве входных данных функции fit() она не будет работать, поскольку ожидает массив (массивоподобных) наблюдений, а не массив целых чисел.
Резюмируя: из этого однострочника вы узнали, как создать первый KNN-регрессор одной строкой кода. Если у вас много меняющихся данных и обновлений модели, то KNN - как раз для вас! А теперь перейдем к безумно популярной сейчас модели машинного обучения: нейронным сетям.
На следующем шаге мы рассмотрим нейросетевой анализ в одной строке кода.
