На этом шаге мы приведем общее описание этого метода.

Популярный алгоритм k-ближайших соседей (K-Nearest Neighbors, KNN) используется для регрессии и классификации во многих приложениях, в частности в рекомендательных системах, а также при классификации изображений и финансовом прогнозе. На нем основаны многие продвинутые алгоритмы машинного обучения (например, предназначенные для информационного поиска). Вне всякого сомнения, понимание KNN - важный элемент качественного обучения в сфере computer science.

Общее описание

Алгоритм KNN - надежный, простой и популярный метод машинного обучения. Несмотря на простоту реализации, это конкурентоспособная и быстрая методика машинного обучения. Во всех прочих моделях машинного обучения, обсуждавшихся выше, обучающие данные использовались для вычисления представления исходных данных, на основе которого затем можно будет предсказывать, классифицировать или кластеризовать новые данные. Например, в алгоритмах линейной и логистической регрессии описываются параметры обучения, в то время как в алгоритме кластеризации вычисляются центры кластеров, исходя из обучающих данных. Алгоритм KNN отличается в этом отношении. В отличие от других подходов, в нем не вычисляется новая модель (или представление), а используется в качестве модели весь набор данных целиком.

Да, все правильно. Модель машинного обучения - всего лишь набор наблюдений. Каждый элемент обучающих данных - часть модели. У такого подхода есть свои преимущества и недостатки. Неудобен он тем, что размеры модели могут резко увеличиваться с ростом объема обучающих данных, а значит, может понадобиться предварительный этап обработки - фильтрации или выборки. Большое преимущество его, впрочем, в относительной простоте этапа обучения (достаточно просто добавить в модель новые значения данных). Кроме того, алгоритм KNN можно использовать как для предсказания, так и для классификации. При заданном входном векторе x алгоритм выглядит следующим образом.

Найти k ближайших соседей x (в соответствии с заранее выбранной метрикой расстояния).
Агрегировать k ближайших соседей в одно значение предсказания или классификации. При этом может использоваться любая агрегирующая функция, например взятие среднего, максимального или минимального значения.

Посмотрим для примера на компанию, торгующую недвижимостью. У нее есть большая база покупателей и цен на дома (рисунок 1).

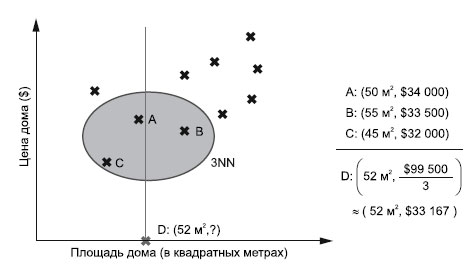
Рис.1. Вычисление цены дома D на основе цен его трех ближайших соседей A, B и C

В один прекрасный момент клиент спрашивает, сколько может стоить дом площадью 52 м². Вы запрашиваете свою модель KNN и немедленно получаете ответ: 33 167 долларов. И действительно, в ту же неделю клиент находит дом за 33 489 долларов. Как же системе KNN удалось произвести настолько безошибочное предсказание?

Прежде всего, система KNN просто вычисляет k = 3 ближайших соседей для запроса D = 52 м² (при использовании евклидового расстояния). Три ближайших соседа: A, B и C с ценами 34 000, 33 500 и 32 000 долларов соответственно. Далее эти три ближайших соседа агрегируются, а именно вычисляется их среднее арифметическое значение. А поскольку в этом примере k = 3, мы назовем нашу модель 3NN. Конечно, можно использовать различные функции подобия, параметр k и метод агрегирования, получая в результате все более изощренные прогностические модели.

Еще одно преимущество KNN - легкость его адаптации к поступающим новым наблюдениям, что справедливо не для всех моделей машинного обучения. Из этого следует очевидный его недостаток - рост вычислительной сложности поиска k-ближайших соседей по мере добавления новых точек данных. Чтобы решить эту проблему, можно непрерывно исключать из модели устаревшие значения. Как мы уже упоминали, с помощью KNN можно также решать задачи классификации. Вместо усреднения по k ближайшим соседям можно использовать механизм голосования: все ближайшие соседи "голосуют" за свои классы, и побеждает класс, за который "отдано больше всего голосов".

На следующем шаге мы закончим изучение этого вопроса.

Предыдущий шаг Содержание Следующий шаг