На этом шаге мы рассмотрим пример получения минимальной дисперсии.

Возможно, вы читали о пяти V больших данных:

объем (volume),
скорость (velocity),
разнообразие (variety),
достоверность (veracity) и
ценность (value)

Иногда выделяют не пять, а три V, а порой даже семь: помимо перечисленных, еще и изменчивость (variability) и визуализацию (visualization).

Дисперсия (variance) - еще одно важное V: это мера ожидаемого (квадратичного) отклонения данных от среднего значения. На практике дисперсия - важный показатель, нашедший свои приложения в финансах, прогнозе погоды и обработке изображений.

Общее описание

Дисперсия - это мера того, насколько данные разбросаны вокруг их среднего значения в одномерном или многомерном пространстве. Чуть ниже вы увидите наглядный пример. Фактически дисперсия - один из важнейших показателей в машинном обучении. Она захватывает обобщенные закономерности в данных, а машинное обучение прежде всего ориентировано на распознавание закономерностей.

В основе многих алгоритмов машинного обучения лежит дисперсия в той или иной форме. Например, подбор правильного соотношения систематической ошибки и дисперсии - хорошо известная задача в машинном обучении: хитроумные модели машинного обучения подвержены риску переобучения (высокая дисперсия), но очень точно отражают обучающие данные (маленькая систематическая ошибка). С другой стороны, простые модели часто хорошо обобщаются (низкая дисперсия), но плохо отражают данные (большая систематическая ошибка).

Что же такое дисперсия? Это простой статистический показатель, отражающий степень разбросанности данных относительно их среднего значения. На рисунке 1 приведен пример в виде графиков двух наборов данных: один с низкой дисперсией, а второй - с высокой.

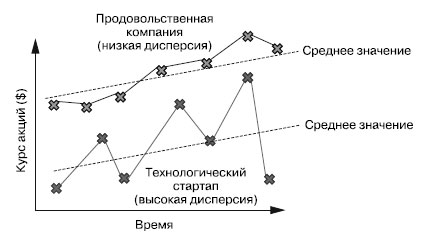
Рис.1. Сравнение дисперсии курсов акций двух компаний

В этом примере показаны курсы акций двух компаний. Курс акций технологического стартапа сильно отклоняется от среднего значения. Курс акций продовольственной компании довольно стабилен и лишь незначительно отклоняется от среднего значения. Другими словами, у технологического стартапа высокая дисперсия, а у продовольственной компании - низкая.

На математическом языке вычислить дисперсию var(X) множества числовых значений X можно с помощью следующей формулы:

   var(X) = ∑ = (x - x_{среднее})
           ^x∈X

Величина x_{среднее} представляет собой среднее значение данных во множестве X.

Код

По мере старения многие инвесторы стремятся сократить общий риск своего инвестиционного портфеля. Согласно доминирующей философии инвестиций, следует стремиться к акциям с более низкой дисперсией как менее рискованным инвестиционным активам. Проще говоря, риск потерять деньги будет ниже при инвестициях в стабильную, предсказуемую, крупную компанию, чем при вложениях в маленький технологический стартап.

Задача однострочника из примера 4.7 - найти в портфеле акции с минимальной дисперсией. При инвестициях в эти акции можно ожидать более низкую общую дисперсию портфеля.

Пример 4.7. Вычисление минимальной дисперсии в одной строке кода

## Зависимости
import numpy as np

## Данные (строки: акции / столбцы: курсы акций)
X = np.array([[25, 27, 29, 30],
              [1, 5, 3, 2],
              [12, 11, 8, 3],
              [1, 1, 2, 2],
              [2, 6, 2, 2]])

## Однострочник
## Поиск акций с наименьшей дисперсией
min_row = min([(i, np.var(X[i, :])) for i in range(len(X))], key=lambda x: x[1])

## Результат
print("Row with minimum variance: " + str(min_row[0]))
print("Variance: " + str(min_row[1]))

Архив с файлом можно взять здесь.

Какими же будут результаты выполнения этого фрагмента кода?

Принцип работы

Как обычно, мы сначала описываем данные, на которых будет работать наш однострочник (см. верхнюю часть примера 4.7). Массив NumPy X содержит пять строк (по одной для каждого вида акций в портфеле), каждая из которых включает четыре значения (курсы акций).

Задача - найти идентификатор и дисперсию акций с минимальной дисперсией. Поэтому внешняя функция нашего однострочника - min(). Мы выполняем ее для последовательности кортежей (a, b), в которых первое значение кортежа а представляет собой индекс строки (индекс вида акций), а второе значение кортежа b - дисперсию строки.

Возможно, вы спросите: а что такое минимальное значение последовательности кортежей? Конечно, необходимо четко определить эту операцию перед использованием. Для этого мы обратимся к аргументу key функции min(). В него должна передаваться функция, получающая последовательность и возвращающая допускающее сравнение объектное значение. Опять же, значения в нашей последовательности - кортежи, и нам нужно найти кортеж с минимальной дисперсией (вторым значением кортежа). А поскольку дисперсия - второе значение в кортеже, мы возвращаем для сравнения х[1]. Другими словами, "победителем" становится кортеж с минимальным вторым значением.

Посмотрим, как создать эту последовательность значений-кортежей. Чтобы создать кортеж для индекса строки (вида акций), мы прибегнем к списковому включению. Первый элемент кортежа - просто индекс строки i. Второй элемент кортежа - дисперсия этой строки. Для вычисления дисперсии строки мы используем функцию var() библиотеки NumPy в сочетании со срезом.

Результат выполнения нашего однострочника выглядит так:

Row with minimum variance: 3 
Variance: 0.25

Хотелось бы добавить, что существует и альтернативный способ решения этой задачи. Возможно, вы предпочтете следующее решение вместо упомянутого однострочника:

var = np.var(X, axis=1)
min_row = (np.where(var==min(var)), min(var))

В первой строке вычисляется дисперсия массива NumPy X по столбцам (axis=1). Во второй создается кортеж. Первое значение кортежа представляет собой индекс минимума в массиве дисперсий. А второе - сам этот минимум в массиве дисперсий. Обратите внимание, что одна и та же (минимальная) дисперсия может быть у нескольких строк.

Такое решение удобнее для восприятия. Поэтому явно необходимо выбирать между лаконичностью и удобочитаемостью кода. Возможность втиснуть что-либо в одну строку кода не означает, что так следует поступать всегда. При прочих равных условиях лучше писать лаконичный и удобочитаемый код, а не раздувать его ненужными определениями, комментариями или промежуточными шагами.

Теперь, изучив в этом разделе основы понятия дисперсии, вы готовы узнать, как вычислять основные статистические показатели.

На следующем шаге мы рассмотрим основные статистические показатели с помощью одной строки кода.

Предыдущий шаг Содержание Следующий шаг