На этом шаге мы приведем некоторый теоретический метериал, отноящийся к изучаемому вопросу.
Исследователю данных, как и специалисту по машинному обучению, необходимо знать основные статистические показатели. Некоторые алгоритмы машинного обучения базируются исключительно на статистических показателях (например, байесовские сети).
Например, вычисление основных статистических показателей матриц (среднего значения, дисперсии или стандартного отклонения) - неотъемлемая составляющая анализа разнообразных наборов данных, в том числе финансовых, медицинских и данных соцсетей. По мере роста популярности машинного обучения и науки о данных умение применять библиотеку NumPy, используемую в Python для исследования данных, статистики и линейной алгебры, становится все более востребованным на рынке.
Из этого однострочника вы увидите, как вычислять основные статистические показатели с помощью NumPy.
Общее описание
Здесь рассказывается, как вычислить среднее значение, стандартное отклонение и дисперсию по одной из осей координат. Вычисления этих трех величин очень похожи; если вы разберетесь с одной, то и остальные будут для вас понятны.
Вот что мы хотим сделать: по заданному массиву NumPy данных об акциях, в котором строки соответствуют различным компаниям, а столбцы - курсам их акций по дням, найти среднее значение и стандартное отклонение курса акций каждой из компаний (рисунок 1).
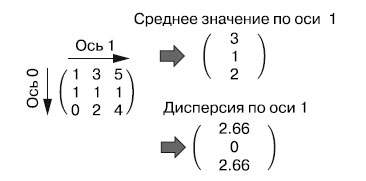
Рис.1. Среднее значение и дисперсия по оси 1
В примере показан двумерный массив NumPy, но на практике массивы бывают намного большей размерности.
Среднее арифметическое, дисперсия, стандартное отклонение
Прежде чем выяснить, как вычислить все это в NumPy, понемногу разберемся со всем, что нужно для этого знать. Пусть нам нужно вычислить просто среднее значение, дисперсию или стандартное отклонение по всем значениям массива NumPy. Вы уже видели ранее примеры вычисления среднего значения и дисперсии. Стандартное отклонение равно просто квадратному корню дисперсии. Вычислить их все легко можно с помощью следующих функций:
import numpy as np X = np.array([[1, 3, 5], [1, 1, 1], [0, 2, 4]]) print(np.average(X)) # 2.0 print(np.var(X)) # 2.4444444444444446 print(np.std(X)) # 1.5634719199411433
Наверное, вы обратили внимание, что функции применяются тут к двумерному массиву NumPy X. Но NumPy просто "сплющивает" этот массив и вычисляет функции на основе полученного результата. Например, среднее арифметическое "сплющенного" массива NumPy X вычисляется следующим образом:
(1 + 3 + 5 + 1 + 1 + 1 + 0 + 2 + 4) / 9 = 18 / 9 = 2.0 .
Вычисление среднего значения, дисперсии, стандартного отклонения по одной из осей
Иногда, впрочем, бывает нужно вычислить эти функции по одной из осей. Для этого можно указать ключевое слово axis в качестве аргумента функций вычисления среднего значения, дисперсии или стандартного отклонения (см. подробное описание аргумента axis на 42 шаге).
На следующем шаге мы закончим изучение этого вопроса.
