На этом шаге мы рассмотрим планарные графы.
Сопоставив вершинам графа точки на плоскости или в пространстве, а ребрам - линии, соединяющие точки, соответствующие концам ребра, можно получить диаграмму - визуальное представление данного графа.
Очевидно, что для любого графа можно построить бесконечное количество таких диаграмм. Если на некоторой диаграмме среди точек, соответствующих вершинам графа, нет совпадающих, а линии, соответствующие ребрам графа, не имеют общих точек (за исключением концов), то эта диаграмма называется геометрической реализацией графа.
- Теорема 1.
- Для любого графа существует геометрическая реализация в трехмерном евклидовом пространстве.
- Доказательство.
-
- реализуем |V| точек, соответствующих вершинам графа, на одной прямой;
- проведем через эту прямую |E| различных полуплоскостей;
- реализуем каждое ребро в своей полуплоскости.
Возникает вопрос: любой ли граф можно реализовать на плоскости? Ответ - отрицательный. Геометрическую реализацию на плоскости допускают лишь некоторые графы; такие графы называются планарными.
Для последующего изложения нам понадобится понятие грани. Неформально определим грань как часть плоскости, на которые плоскость "разрезается" линиями геометрической реализации графа. Всегда существует неограниченная внешняя грань.
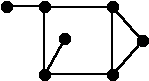
Рис.1. Пример графа
На приведенном рисунке изображен граф, у которого 7 вершин, 8 ребер, 3 грани.
На следующем шаге мы рассмотрим формулу Эйлера.
