На этом шаге мы рассмотрим формулу Эйлера.

Формула Эйлера.

Для любой геометрической реализации графа G=(V,E) на плоскости верно: p-q+r=2, где p=|V|, q=|E|, r - число граней (без доказательства).

Теорема 2.

Если в связном планарном графе нет циклов длины меньше k и k=3, то q<=k(p-2)/(k-2), где p=|V|, q=|E|.

Доказательство (не совсем формальное).

Пусть граф реализован на плоскости и при этом получилось r граней. Пусть q_i - число сторон в i-й грани (см. рисунок 1). Каждое ребро является стороной двух граней, поэтому 2q=Sum(q_i, i=1...r). По условию в графе нет циклов длины меньше k, но тогда q_i=k (т.к. стороны грани образуют цикл) и 2q=Sum(q_i, i=1..r)-k*r. По формуле Эйлера r=2-p+q, следовательно, 2q=k*(2-p+q), из чего следует доказываемое неравенство.

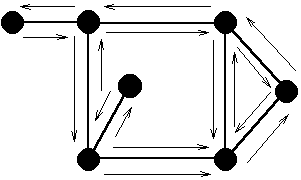
Рис.1. Пример графа

Граф на рисунке 1 имеет 8 ребер, 3 грани, 3+6+7=16 сторон.

Следствие 1 теоремы 2.

Для любого связного планарного графа без петель и кратных ребер выполняется неравенство: q<=3(p-2), где p=|V|, q=|E|.

Доказательство.

Т.к. по условию в графе нет петель и кратных ребер, в нем нет и циклов длины меньше 3, поэтому, подставляя k=3 в неравенство теоремы 2, получаем: q<=k(p-2)/(k-2)=3(p-2).

Теорема 3.

Граф K₅ не планарен.

Доказательство.

K₅ связен, в нем нет петель и кратных ребер, но следствие 1 теоремы 2 не выполняется - q=10>3(p-2)=9. Значит, K₅ не планарен.

Теорема 4.

Граф K₃₃ не планарен.

Доказательство.

Замечание: использование следствия 1 теоремы 2 здесь не поможет, т.к. q=9<3(p-2)=12. В K₃₃ нет циклов длины меньше 4, поэтому применим неравенство теоремы 2 непосредственно (при k=4): q=9>4(p-2)/2=8. Следовательно, K₃₃ не планарен.

Теорема Понтрягина-Куратовского (критерий планарности графов).: Граф G планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных K₅ или K₃₃.
Доказательство.: Необходимость следует из утверждений 1-4 (см. ниже), а также из того факта, что графы K₅ и K₃₃ не планарны (в соответствии с теоремами 3 и 4).
Утверждение 1.: Если графы U₁ и U₂ изоморфны, то U₁ планарен тогда и только тогда, когда U₂ планарен.
Доказательство.: Любая геометрическая реализация U₁ является геометрической реализацией U₂, и наоборот.
Утверждение 2.: Любое подразделение U' графа U планарно тогда и только тогда, когда U планарен.
Доказательство.: (=>) граф U' планарен, следовательно, существует его геометрическая реализация на плоскости R'. Построим по R' плоскую геометрическую реализацию R графа U. Для этого объединим все линии R', соответствующие ребрам U', полученным в результате выполнения операций подразделения ребер. В силу существования R граф U является планарным.
(<=) граф U планарен, следовательно, существует его геометрическая реализация на плоскости R. Построим по R плоскую геометрическую реализацию R' графа U'. Для этого повторим в любой последовательности операции подразделения ребер, которые привели к построению U'. После выполнения каждой из этих операций будем разбивать линию, соответствующую подразделяемому ребру, на две линии (разбиение можно производить в любой точке, не совпадающей с концами линии). В силу существования R' граф U' является планарным.
Утверждение 3.: Если графы U₁ и U₂ гомеоморфны, то U₁ планарен тогда и только тогда, когда U₂ планарен.
Доказательство.: (=>) по условию U₁ и U₂ гомеоморфны (по определению), поэтому существуют их изоморфные подразделения U₁' и U₂'. По условию граф U₁ планарен {по утв.2}, граф U₁' планарен {по утв.1}, поэтому изоморфный ему граф U₂' планарен {по утв.2}, следовательно граф U₂ планарен.
(<=) аналогично.
Утверждение 4.: Если подграф U' графа U не планарен, то U также не планарен.
Доказательство.: Допустим, что граф U планарен. Следовательно, существует его плоская геометрическая реализация R. Но тогда можно построить плоскую геометрическую реализацию R' графа U': для этого достаточно удалить из R точки и линии, соответствующие тем вершинам и ребрам U, которых нет в U'. Из существования R' следует, что U' планарен - получили противоречие.
Достаточность теоремы доказывается гораздо сложнее.

Существуют и другие критерии планарности графов.

На следующем шаге мы рассмотрим раскраски графов.

Предыдущий шаг Содержание Следующий шаг