На этом шаге мы рассмотрим равномерное алфавитное двоичное кодирование; байтовый код.
В этом случае двоичный код первичного
алфавита строится цепочками равной длины, т.е. со всеми знаками связано
одинаковое количество информации равное I0. Передавать признак конца
знака не требуется, поэтому для определения длины кодовой цепочки можно
воспользоваться формулой:
K(2) 
log2N.
Приемное устройство просто отсчитывает оговоренное заранее количество
элементарных сигналов и интерпретирует цепочку (устанавливает, какому знаку она
соответствует). Правда, при этом недопустимы сбои, например, пропуск
(непрочтение) одного элементарного сигнала приведет к сдвигу всей кодовой
последовательности и неправильной ее интерпретации; решается проблема путем
синхронизации передачи или иными способами. С
другой стороны, применение равномерного кода оказывается одним из средств
контроля правильности передачи, поскольку факт поступления лишнего элементарного сигнала или, наоборот, поступление неполного кода сразу
интерпретируется как ошибка.
Примером равномерного алфавитного
кодирования является телеграфный код Бодо, пришедший на смену азбуке Морзе.
Исходный алфавит должен содержать не более 32-х символов; тогда K(2)
= log2 32 = 5, т.е. каждый знак содержит 5 бит информации. Условие N
32,
очевидно, выполняется для языков, основанных на латинском алфавите
(N = 27 = 26+”пробел”), однако в русском алфавите 34 буквы (с пробелом) – именно по этой
причине пришлось "сжать" алфавит (как в коде Хаффмана) и объединить в один знак
"е" и "ё", а также "ь" и "ъ". После такого сжатия N = 32, однако, не остается свободных кодов для
знаков препинания, поэтому в телеграммах они отсутствуют или заменяются
буквенными аббревиатурами; это не является заметным ограничением, поскольку,
как указывалось выше, избыточность языка позволяет легко восстановить
информационное содержание сообщения. Избыточность кода Бодо для русского языка
Q(r) = 0,129, для английского Q(e) = 0,193.
Другим важным для нас примером использования равномерного алфавитного кодирования является представление символьной информации в компьютере. Чтобы определить длину кода, необходимо начать с установления количество знаков в первичном алфавите. Компьютерный алфавит должен включать:
- 26
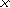2=52
букв латинского алфавита (с учетом прописных и строчных);
- 33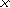2=66
букв русского алфавита;
- цифры 0...9 – всего 10;
- знаки математических операций, знаки препинания, спецсимволы
20.
Получаем, что общее число символов N 
148.
Теперь можно оценить длину кодовой цепочки: K(2) log2148
7,21.
Поскольку K(2) должно быть целым, очевидно, K(2)= 8.
Именно такой способ кодирования принят в компьютерных системах: любому символу
ставится в соответствие цепочка из 8 двоичных разрядов (8 бит). Такая цепочка
получила название байт, а представление таким образом символов – байтовым
кодированием.
Байт наряду с битом может использоваться как единица измерения количества информации в сообщении. Один байт соответствует количеству информации в одном символе алфавита при их равновероятном распределении. Этот способ измерения количества информации называется также объемным. Пусть имеется некоторое сообщение (последовательность знаков); оценка количества содержащейся в нем информации согласно рассмотренному ранее вероятностному подходу (с помощью формулы Шеннона ) дает Iвер, а объемная мера пусть равна Iоб; соотношение между этими величинами:
Iвер Iоб
Именно байт принят в качестве единицы измерения количества информации в международной системе единиц СИ. 1 байт = 8 бит. Наряду с байтом для измерения количества информации используются более крупные производные единицы:
1 Кбайт = 210 байт = 1024 байт (килобайт)
1 Мбайт = 220 байт = 1024 Кбайт (мегабайт)
1 Гбайт = 230 байт = 1024 Мбайт (гигабайт)
1 Тбайт = 240 байт = 1024 Гбайт (терабайт)
Использование 8-битных цепочек позволяет закодировать 28=256 символов, что превышает оцененное выше N и, следовательно, дает возможность употребить оставшуюся часть кодовой таблицы для представления дополнительных символов.
Однако недостаточно только условиться об определенной длине кода. Ясно, что способов кодирования, т.е. вариантов сопоставления знакам первичного алфавита восьмибитных цепочек, очень много. По этой причине для совместимости технических устройств и обеспечения возможности обмена информацией между многими потребителями требуется согласование кодов. Подобное согласование осуществляется в форме стандартизации кодовых таблиц. Первым таким международным стандартом, который применялся на больших вычислительных машинах, был EBCDIC (Extended Binary Coded Decimal Interchange Code) – "расширенная двоичная кодировка десятичного кода обмена". В персональных компьютерах и телекоммуникационных системах применяется международный байтовый код ASCII (American Standard Code for Information Interchange – "американский стандартный код обмена информацией"). Он регламентирует коды первой половины кодовой таблицы (номера кодов от 0 до 127, т.е. первый бит всех кодов 0). В эту часть попадают коды прописных и строчных английских букв, цифры, знаки препинания и математических операций, а также некоторые управляющие коды (номера от 0 до 31). Ниже приведены некоторые ASCII-коды:
| Знак, клавиша | Код двоичный | Код десятичный |
|---|---|---|
| пробел | 00100000 | 32 |
| A (лат) | 01000001 | 65 |
| B (лат) | 01000010 | 66 |
| Z | 01011010 | 90 |
| 0 | 00110000 | 48 |
| 1 | 00110001 | 49 |
| 9 | 00111001 | 57 |
| Клавиша ESC | 00011011 | 27 |
| Клавиша Enter | 00001101 | 13 |
Вторая часть кодовой таблицы – онасчитается расширением основной – охватывает коды в интервале от 128 до 255 (первый бит всех кодов 1). Она используется для представления символов национальных алфавитов (например, русского или греческого), а также символов псевдографики. Для этой части также имеются стандарты, например, для символов русского языка это КОИ–8, КОИ–7 и др.
Как в основной таблице, так и в ее расширении коды букв и цифр соответствуют их лексикографическому порядку (т.е. порядку следования в алфавите) – это обеспечивает возможность автоматизации обработки текстов и ускоряет ее.
В настоящее время появился и находит все более широкое применение еще один международный стандарт кодировки – Unicode. Его особенность в том, что в нем использовано 16-битное кодирование, т.е. для представления каждого символа отводится 2 байта. Такая длина кода обеспечивает включения в первичный алфавит 65536 знаков. Это, в свою очередь, позволяет создать и использовать единую для всех распространенных алфавитов кодовую таблицу.
На следующем шаге мы рассмотрим алфавитное кодирование с неравной длительностью элементарных сигналов. Код Морзе.
