На этом шаге мы рассмотрим кодирование с неравной длительностью элементарных сигналов. Код Морзе.
В качестве примера использования
данного варианта кодирования рассмотрим телеграфный код Морзе ("азбука Морзе").
В нем каждой букве или цифре сопоставляется некоторая последовательность
кратковременных импульсов – точек и тире, разделяемых паузами. Длительности
импульсов и пауз различны: если продолжительность импульса, соответствующего
точке, обозначить ![]() , то длительность импульса тире составляет
3
, то длительность импульса тире составляет
3![]() ,
длительность паузы между точкой и тире
,
длительность паузы между точкой и тире ![]() , пауза
между буквами слова 3
, пауза
между буквами слова 3![]() , пауза
между словами (пробел) – 6
, пауза
между словами (пробел) – 6![]() . Таким
образом, под знаками кода Морзе следует понимать:
"
. Таким
образом, под знаками кода Морзе следует понимать:
"![]() " –
"короткий импульс + короткая пауза",
"
" –
"короткий импульс + короткая пауза",
"![]() " –
"длинный импульс + короткая пауза", "0" – "длинная пауза", т.е. код оказывается
троичным.
" –
"длинный импульс + короткая пауза", "0" – "длинная пауза", т.е. код оказывается
троичным.
Свой код Морзе разработал в 1838 г., т.е. задолго до исследований относительной частоты появления различных букв в текстах. Однако им был правильно выбран принцип кодирования – буквы, которые встречаются чаще, должны иметь более короткие коды, чтобы сократить общее время передачи. Относительные частоты букв английского алфавита он оценил простым подсчетом литер в ячейках типографской наборной машины. Поэтому самая распространенная английская буква "E" получила код "точка". При составлении кодов Морзе для букв русского алфавита учет относительной частоты букв не производился, что, естественно, повысило его избыточность. Как и в рассмотренных ранее вариантах кодирования, произведем оценку избыточности. По-прежнему для удобства сопоставления данные представим в приведенном ниже формате. Признак конца буквы ("0") в их кодах не отображается, но учтен в величине ki – длине кода буквы i.
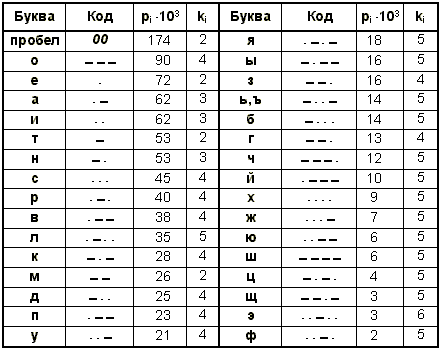
Среднее значение длины кода K(3) = 3,361. Полагая появление знаков вторичного алфавита равновероятным, получаем среднюю информацию на знак равной I(2) = log23 = 1,585 бит. Подставляя эти данные, а также для русского алфавита I1(1) = 4,356 бит в (2), получаем:
Q(r) = 1 – 4,356/(3,361 – 1,585)
![]() 0,182
0,182
т.е. избыточность
составляет около 18% (для английского языка
![]() 15%). Тем
не менее, код Морзе имел в недалеком прошлом весьма широкое распространение в
ситуациях, когда источником и приемником сигналов являлся человек (не
техническое устройство) и на первый план выдвигалась не экономичность кода, а
удобство его восприятия человеком.
15%). Тем
не менее, код Морзе имел в недалеком прошлом весьма широкое распространение в
ситуациях, когда источником и приемником сигналов являлся человек (не
техническое устройство) и на первый план выдвигалась не экономичность кода, а
удобство его восприятия человеком.
На следующем шаге мы рассмотрим блочное двоичное кодирование.
