На этом шаге мы рассмотрим перевод чисел между системами счисления 2 – 8 – 16. .

Интерес к двоичной системе счисления вызван тем, что именно эта система используется для представления чисел в компьютере. Однако двоичная запись оказывается громоздкой, поскольку содержит много цифр, и, кроме того, она плохо воспринимается и запоминается человеком из-за зрительной однородности (все число состоит из нулей и единиц). Поэтому в нумерации ячеек памяти компьютера, записи кодов команд, нумерации регистров и устройств и пр. используются системы счисления с основаниями 8 и 16; выбор именно этих систем счисления обусловлен тем, что переход от них к двоичной системе и обратно осуществляется, как будет показано ниже, весьма простым образом.

Двоичная система счисления имеет основанием 2 и, соответственно, 2 цифры: 0 и 1.

Восьмеричная система счисления имеет основание 8 и цифры 0, 1, ..., 7.

Шестнадцатеричная система счисления имеет основание 16 и цифры 0, 1, ..., 9, A, B, C, D, E, F. При этом знак A является 16-ричной цифрой, соответствующей числу 10 в десятичной системе; B₁₆ = 11₁₀; C₁₆ = 12₁₀; D₁₆ = 13₁₀; E₁₆ = 14₁₀; F₁₆ = 15₁₀. Другими словами, в данном случае A ... F - это не буквы латинского алфавита, а цифры 16-ричной системы счисления и поэтому они имеют только такое начертание (не могут быть представлены в виде, например, соответствующих строчных букв, как в текстах).

Пользуясь алгоритмами, сформулированными в предыдущих разделах, можно заполнить таблицу:

Таблица 1. Представление числе в разных системах счисления
Десятичная Двоичная Восьмеричная Шестнадцатеричная

0 0 0 0

1 1 1 1

2 10 2 2

3 11 3 3

4 100 4 4

5 101 5 5

6 110 6 6

7 111 7 7

8 1000 10 8

9 1001 11 9

10 1010 12 A

11 1011 13 B

12 1100 14 C

13 1101 15 D

14 1110 16 E

15 1111 17 F

Таблица 1. **Представление числе в разных системах счисления**
Десятичная	Двоичная	Восьмеричная	Шестнадцатеричная
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

Докажем две теоремы.

Теорема 1.

Для преобразования целого числа Z_p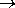Z_q в том случае, если системы счисления связаны соотношением q = p^r, где r - целое число большее 1, достаточно Z_p разбить справа налево на группы по r цифр и каждую из них независимо перевести в систему q.

Доказательство.

Пусть максимальный показатель степени в записи числа p по форме (1) равен k-1, причем, 2r>k-1>r.

Z_p = (a_k-1…a₁a₀)_p = a_k-1·p^k-1 + a_k-2·p^k-2 + ……+ a_j·p^j +…+ a₁·p¹ + a₀·p⁰

Вынесем множитель p^r из всех слагаемых, у которых j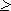r. Получим:

Z_p = (a_k-1·p^k-1-r+ a_k-2·p^k-2-r +… + a_r·p⁰)·p^r + (a_r-1·p^r-1 +… + a₀·p⁰)·p⁰ = b₁·q¹ + b₀·q⁰, где

b₁ = a_k-1·p^k-1-r + … + a_r·p⁰ = (a_k-1…a_r )_p

b₀ = a_r-1·p^r-1 +… + a₀·p⁰ = (a_r-1…a₀)_p

Таким образом, r-разрядные числа системы с основанием p оказываются записанными как цифры системы с основанием q. Этот результат можно обобщить на ситуацию произвольного k-1>r - в этом случае выделится не две, а больше (m) цифр числа с основанием q. Очевидно, Z_q = (b_m … b₀ )_q.

Пример 6. Выполнить преобразование Z2 = 110001₂

Z8.

Исходное число разбивается на группы по три разряда справа налево (8 = 23, следовательно, r = 3) и каждая тройка в соответствии с таблицей 1 переводится в 8-ричную систему счисления независимо от остальных троек:

Следовательно, 110001₂ = 61₈ . Аналогично, разбивая Z₂ на группы по 4 двоичные цифры и дополняя старшую группу незначащими нулями слева, получим 110001₂= 31₁₆.

Теорема 2.

Для преобразования целого числа Z_p 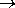Z_q в том случае, если системы счисления связаны соотношением p = q^r, где r - целое число большее 1, достаточно каждую цифру Z_p заменить соответствующим r-разрядным числом в системе счисления q, дополняя его при необходимости незначащими нулями слева до группы в r цифр.

Доказательство.

Пусть исходное число содержит две цифры, т.е.

Z_p = (a₁a₀)_p = a₁·p¹ + a₀·p⁰.

Для каждой цифры справедливо: 0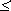a_i 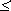p-1 и поскольку p = q^r, 0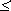a_i 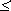q^r -1, то в представлении этих цифр в системе счисления q максимальная степень многочленов (1) будет не более r - 1 и эти многочлены будут содержать по r цифр:

a₁ = b_r-1⁽¹⁾·q^r-1+b_r-2⁽¹⁾·q^r-2+…+₀⁽¹⁾·q⁰

a₀ = b_r-1⁽⁰⁾·q^r-1+b_r-2⁽⁰⁾·q^r-2+…+₀⁽⁰⁾·q⁰

Тогда:

Z_p = (a₁a₀)_p = (b_r-1⁽¹⁾·q^r-1+…+b₀⁽¹⁾·q⁰)·q^r+(b_r-1⁽⁰⁾·q^r-1+…+b₀⁽⁰⁾·q⁰)·q⁰ =
= b_r-1⁽¹⁾·q^2r-1+…+b₀^{(1 )}·q^r+b_r-1⁽⁰⁾·q^r-1+…+b₀⁽⁰⁾·q⁰ = (b_r-1⁽¹⁾…b₀⁽⁰⁾)_q = Z_q

причем, число Z_q содержит 2r цифр. Доказательство легко обобщается на случай произвольного количества цифр в числе Z_p.

Пример 7. Выполнить преобразование D3₁₆Z₂.

Переходы Z₈ Z₁₆ и Z₁₆ Z₈, очевидно, удобнее осуществлять через промежуточный переход к двоичной системе. Например, 123₈ = 001010011₂ = 53₁₆.

На следующем шаге мы рассмотрим преобразование нормализованных чисел.

Предыдущий шаг Содержание Следующий шаг