На этом шаге мы рассмотрим производные операции над функциями.

Кроме операции подстановки и примитивной рекурсии, которые являются основными, используются и другие операции, которые сохраняют свойства примитивной рекурсивности функций, их называют производными и они получаются из основных операций и базы элементарных функций.

Пусть задана совокупность функций Ψ = {Ψ₁, Ψ₂, ..., Ψ_n} и в результате некоторой операции над этими функциями получена функция φ = F(Ψ₁, Ψ₂, ..., Ψ_n).

Определение. Операция F называется примитивно рекурсивной операцией, если из равенства φ = F(Ψ₁, Ψ₂, ..., Ψ_n) следует, что функция φ есть ПРФ относительно совокупности Ψ.

Рассмотрим несколько примеров.

1. Пусть задана некоторая функция g(x,y) и функция φ(x,y,z) = g(x,y).

В этом случае говорят, что функция φ получена из функции g с помощью операции введения фиктивной переменной, именно, введением фиктивной переменной z. При этом функция φ(x,y,z) является ПРФ относительно совокупности {g}. Действительно, φ можно представить следующим образом:

φ(x,y,z) = g(I₁³(x,y,z), I₂³(x,y,z)).

Как видим, функция φ получена из функции g и I₁³, I₂³ операцией подстановки, т.е. φ = S(g, I₁³, I₂³).

2. Пусть задана функция g(x,y,z) и если φ(x,y) = g(x,y,a), то говорят, что функция Ψ получена из функции g с помощью операции замены константы.

Действительно φ(x,y) можно представить следующим образом:

и называется она операцией замены константы.

3. Пусть задана функция g(x,y) и φ(x,y) = g(y,x), то говорят, что функция φ получена из функции g с применением операции перестановки переменных. Действительно, функцию φ(x,y) можно представить следующим образом:

4. Пусть дана функция g(x) и φ(x) = g(x,x), то говорят, что функция φ получена из функции g с помощью операции отождествленной переменной. Действительно, функцию φ можно представить следующим образом:

т.е.

5. Пусть заданы функции g, h₁, h₂, ..., h_k, где h_i, i = 1, 2, ..., k - некоторые функции различного количества переменных. Если φ = g(h₁, h₂, ..., h_k), то говорят, что функция φ получена из функции g с помощью операции произвольной подстановки (суперпозиции).

Например, пусть имеются функции g(x₁,x₂,x₃), h₁(x), h₂(x,y), h₃(x,y,z) и φ(x,y,z) = g(h₁(x), h₂(x,y), h₃(x,y,z)).

Тогда функция φ является ПРФ относительно совокупности {g, h₁, h₂, h₃}.

Покажем, что данная операция справедлива. Функцию φ можно представить следующим образом:

Введем следующие обозначения:

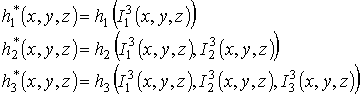
Как видим, функции h₁^*, h₂^* получены из функций h₁, h₂ соответственно операцией введения фиктивных переменных. Поэтому h₁^* является ПРФ относительно совокупности {h₁} и h₂^* - ПРФ относительно совокупности {h₂}. Очевидно, h₃^* - ПРФ относительно совокупности {h₃}. Тогда функция φ приобретает вид:

Следовательно, она ПРФ относительно совокупности {g, h₁^*, h₂^*, h₃^*}. Учитывая свойство 1 относительно примитивной рекурсивности, получаем, что функция φ - ПРФ относительно совокупности {g, h₁, h₂, h₃}.

На следующем шаге мы рассмотрим операции конечного суммирования и конечного произведения.

Предыдущий шаг Содержание Следующий шаг