Шаг 8.
Понятие рекурсии.
Операции конечного суммирования и конечного произведения

    На этом шаге мы рассмотрим операции конечного суммирования и конечного произведения .

    Пусть задана функция g(x₁, x₂, ..., x_n, y).

    Определение. Говорят, что функция σ(x₁, x₂, ..., x_n, z) получена из функции g(x₁, x₂, ..., x_n, y) с применением операции конечного суммирования, если для любого набора переменных (x₁, x₂, ..., x_n, z) выполняется следующее равенство:

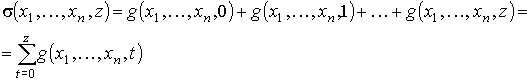(1)

    Определение. Говорят, что функция δ(x₁, x₂, ..., x_n, z) получена из функции g(x₁, x₂, ..., x_n, y) с применением операции конечного произведения, если для любого набора переменных (x₁, x₂, ..., x_n, z) выполняется следующее равенство:

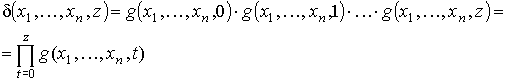(2)

Теорема 1.

Операции конечного суммирования и конечного произведения сохраняют свойство примитивной рекурсивности функции.

Доказательство.

Приведем доказательство относительно операции конечного суммирования (аналогично доказывается относительно операции конечного произведения).

    Пусть

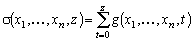
    Тогда по определению операции примитивной рекурсии получим:

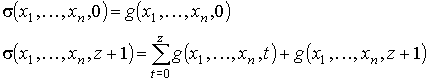
    Таким образом, функция σ получается операцией примитивной рекурсии из функции g' и h(x₁, ..., x_n, z, u), т.е. σ = R(g',h).

    Действительно

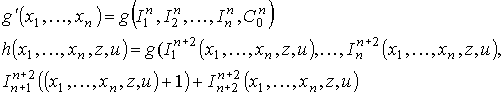
    Очевидно, что

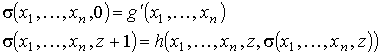
    Из задания функций g' и h следует, что они являются ПРФ соответственно относительно совокупности {g}. Функция σ - ПРФ относительно функций g' и h. Следовательно, операция конечного суммирования сохраняет свойство примитивной рекурсивности функции. Что требовалось доказать.

---

    Пример. Дана функция:

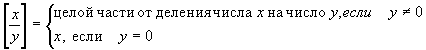
    Покажем, что данная функция является примитивно рекурсивной. Для доказательства ПРФ данной функции используем операцию конечного суммирования.

    Рассмотрим два случая:

• пусть y>0 . Введем обозначения:

  

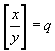
      Тогда по теореме о делении с остатком,

  

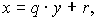
  где 0<=r<=y. Очевидно, что число q удовлетворяет соотношениям:

  

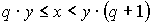
      Рассмотрим следующие разности:

  

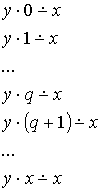
      Нетрудно подсчитать, что число нулей в этой последовательности равно q+1.

      Поэтому, исходя из вышеуказанной разности, q можно выразить следующим образом:

  

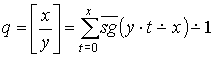
• пусть y=0. В этом случае, функция - может быть получена из функции:

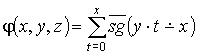  (4)

  операцией отождествленных переменных, т.е.

  

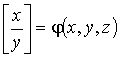
      Таким образом, исходя из того, что:

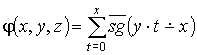  - ПРФ

  и операция отождествленных переменных сохраняет свойство примитивной рекурсивности функций, следует, что:

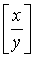  - ПРФ.

    На следующем шаге мы рассмотрим понятие предиката и логической функции. Логические операции с предикатами.

Предыдущий шаг Содержание Следующий шаг