На этом шаге мы рассмотрим операцию ограниченной минимизации.
Пусть задан всюду определенный предикат p(x1, ..., xn, y).
Определение. Говорят, что функция φ(x1, ..., xn, z) получена из предиката p(x1, ..., xn, y) в результате операции ограниченной минимизации, т.е. φ(x1, ..., xn, z) = μγy<=zp(x1, ..., xn, y), если выполняются следующие равенства:
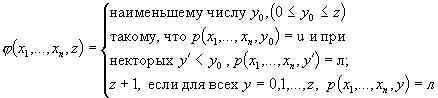(33)
- Теорема 5.
- Функция φ(x1, ..., xn, z), полученная из предиката p(x1, ..., xn, y) в результате операции ограниченной минимизации, является примитивно рекурсивной функцией относительно {p}.
- Доказательство.
- Пусть задан всюду определенный предикат p(x1, ..., xn, y) и h(x1, ..., xn, y) - представляющая функция
данного предиката и пусть φ(x1, ..., xn, z) = μγy<=zp(x1, ..., xn, y).
Покажем, что φ(x1, ..., xn, z) можно представить в виде:
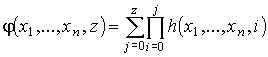(34).
Действительно это равенство имеет место.
1) Пусть φ(x1, ..., xn, z) = y0, тогда p(x1, ..., xn, y0) = и для всех y<y0 p(x1, ..., xn, y) = л. Следовательно:
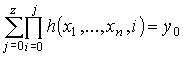
2) Пусть φ(x1, ..., xn, z) = z + 1. Тогда по определению операции ограниченной минимизации p(x1, ..., xn, y) = k для всех y, где 0<=y<=z. Следовательно, в правая часть формуле (1), равна z+1 единиц.
Таким образом, из пунктов 1-2 следует, что формула (34) удовлетворяет заданию функции с помощью операции ограниченной минимизации. Так как операции конечного произведения и конечного суммирования сохраняют свойства примитивной рекурсивности функцией, то получаем, что функция φ(x1, ..., xn, z) является ПРФ относительно {p}.
Следствие. Операция ограниченной минимизации сохраняет свойство примитивной рекурсивности функций.
Пример. Пусть задана логическая функция p(x), значением которой на произвольном аргументе x является простое число с номером x т.е. p(x) = px (35), где x = 0, 1, 2 , 3, ..., n. Требуется доказать, что она является ПРФ.
Решение. Из курса элементарной математики нам известно, что p является простым числом, если оно имеет в точности два различных делителя.
Между множеством натуральных чисел и множеством простых чисел устанавливаем взаимно однозначное соответствие:
n 0 1 2 3 4 5 ...
px 2 3 5 7 11 13 ...
Покажем, что (35) - ПРФ.
Прежде всего, рассмотрим следующий предикат: pγ(x) = (x - простое число) и определим, что он является примитивно рекурсивным. Для этого сначала докажем, что следующие арифметические функции являются примитивно рекурсивным:
(36)
(37)
Используя ранее доказанные ПРФ, т.е.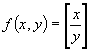 
, легко можно показать, что обе функции являются ПРФ.
Действительно, их соответственно можно представить:
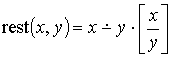(38)
и
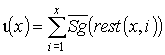. (39)
Следовательно, они являются ПРФ.
Очевидно, представляющей функцией для предиката pγ(x) = (x - простое число) является функция вида:
, (40)
которая является ПРФ.
Из курса теории чисел известно, что имеет место соотношение: 
.
Рассмотрим следующий предикат:
. (41)
Как видно, этот предикат является примитивно рекурсивным как конъюнкция двух примитивно рекурсивных предикатов. Очевидно, если применить к предикату R(y,t) = [(y>t) ∧ pγ(y)], операцию ограниченной минимизации, то получим примитивно рекурсивную функцию. (Это следует, из того что кусочное задание функции сохраняет свойство примитивной рекурсивности функции). Полученную функцию обозначим через φ(z,t), т.е. φ(z,t) = μγy<=zR(y,t). (42)
Применяем к данной функции операцию суперпозиции, точнее вместо z в данном равенстве подставляем
и полученную функцию обозначим через φ0, т.е.
. (43)
Так как операция суперпозиции сохраняет свойство примитивной рекурсивности функций, то φ0 - ПРФ.
Теперь покажем, что логическая функция p(x) - есть результат операции примитивной рекурсии над функциями:
, т.е.
.
Действительно, по определению операции примитивной рекурсии:
.
Предположим, что для некоторого x верно, что p(x) = px. Покажем, что тогда p(x+1) = px+1.
Очевидно, из определения операции примитивной рекурсии следует, что p(x+1) = φ0(x, p(x)),
но из задания функции φ0 следует, что значением
φ0(x,p(x)) является наименьшее простое число y,
большее, чем p(x) и не превосходящее 
; но это и есть простое число с номером x+1, т.е. px+1.
Таким образом, функция (35), как результат операции примитивной рекурсии над ПРФ, сама является примитивно рекурсивной функцией.
На следующем шаге мы рассмотрим частично рекурсивные функции.
