На этом шаге мы рассмотрим частично рекурсивные функции.

Пусть задана функция f(x₁, ..., x_n, y).

Определение. Говорят, что φ(x₁, ..., x_n) получена из f(x₁, ..., x_n, y) с применением операции ограниченной минимизации, если имеет место следующее равенство:

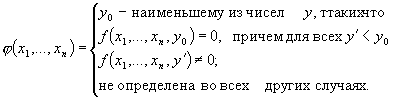(44)

и обозначают φ(x₁, ..., x_n) = μγ(f(x₁, ..., x_n, y) = 0). (45)

Лемма 2.

Операция ограниченной минимизации сохраняет свойство примитивной рекурсивности функции.

Действительно, если имеется алгоритм A_f, вычисляющий функции f(x₁, ..., x_n, y), то есть и алгоритм A_φ, вычисляющий функции φ(x₁, ..., x_n).

Доказательство.

Пусть требуется вычислить значение функции φ на произвольном наборе (x₁, ..., x_n).

Применим алгоритм A_f к набору (x₁, ..., x_n, 0). Если через конечное число шагов алгоритм завершает свою работу результативно, т.е. вычислено значение f(x₁, ..., x_n, 0) и f(x₁, ..., x_n, 0) = 0, то значение функции φ на наборе (x₁, ..., x_n) считаем равным 0. Если f(x₁, ..., x_n, 0) <> 0, то переходим к следующему этапу, на котором применяем алгоритм A_f к набору (x₁, ..., x_n, 1).

Если через конечное число шагов алгоритм завершает свою работу на данном наборе результативно, т.е. вычислено значение f(x₁, ..., x_n, 1) и f(x₁, ..., x_n, 1) = 0, то значение функции φ на наборе считаем равным 1. Если f(x₁, ..., x_n, 1) <> 0, то переходим к следующему этапу и т.д.

Если на (t+1) шаге вычислено значение f(x₁, ..., x_n, t) и f(x₁, ..., x_n, t) = 0, то значение функции φ на наборе (x₁, ..., x_n) считаем равным t. Если f(x₁, ..., x_n, t) <> 0, то переходим к следующему этапу.

В случае, когда алгоритм A_f завершает свою работу на каком-то этапе безрезультативно, или работает бесконечно, то будем считать, что значение φ не определено на данном наборе, т.е. на наборе (x₁, ..., x_n).

Пример 1. Пусть

Тогда

т.е. функция φ(x) только при y = x принимает значение нуль.

Пример 2. Пусть f(x,y) = |x - 2y|. Определим φ(x) = μγ[|x - 2y| = 0].

Очевидно, что функция φ определена только на числах вида 2k, k = 0, 1, 2, ...; и для каждого из них φ(2k) = k.

Пример 3. В качестве примера не всюду определенной функции можно привести следующую функцию:

Действительно, при этом функция φ(x) не определена во всех натуральных наборах, так как φ(x) = μγ[C₈²(x,y) = 0]- не имеет места ни для одного y. Следовательно, будем говорить, что φ(x) - нигде не определенная функция.

Из этих примеров следует, что операция минимизации, вообще говоря, не сохраняет свойство всюду определенности функции (примеры 2, 3) и наоборот, применение операции минимизации к функции не везде определенной может дать всюду определенную функцию (пример 1).

Определение. Частично рекурсивным описанием (ЧРО) функции f называется конечная последовательность функций φ₁, ..., φ_k, удовлетворяющих следующим условиям:

φ_k = f;
Для любого i, 1<=i<=k, φ_k - является либо элементарной функцией, либо получается из предшествующей ей последовательности функций с помощью одной из операций: подстановки, примитивной рекурсии или ограниченной минимизации.

Определение. Функция f называется ЧРФ, если существует ее ЧРО.

Определение. Функция f называется общерекурсивной, если она ЧРФ и всюду определена. (Такие функции еще называют тотальными или просто рекурсивными.)

Не трудно показать, что всякая частично рекурсивная функция алгоритмически вычислима и операции подстановки, примитивной рекурсии и минимизации сохраняют свойству алгоритмическую вычислимость функций.

Очевидно, каждая примитивно рекурсивная функция является частично рекурсивной, но обратное неверно.

Введем обозначения:

K_ПРФ - класс примитивно рекурсивных функций;
K_ОРФ - класс общерекурсивных функций;
K_ЧРФ - класс частично рекурсивных функций.

Тогда между этими классами имеется соотношения:

K_ПРФ ⊆ K_ОРФ ⊆ K_ЧРФ.

Таким образом, класс ЧРФ - самый богатый из построенных классов вычислимых функций и имеет место следующее включение:

K_ЧРФ ⊆ К_ВФ,

где К_ВФ - класс вычислимых функций.

Тезис Черча-Клини представляет гипотезу, из которой следует обратное включение, т.е.

К_ВФ ⊆ K_ЧРФ

Таким образом, класс алгоритмически вычислимых функций совпадает с классом частично рекурсивных функций. Как уже отмечались, это утверждение не может быть доказанным, так как в нем участвует понятие вычислимой функции. Тем не менее можно привести следующие два довода в пользу тезиса Черча - Клини:

достаточно богатый набор примеров арифметических функций, интуитивно алгоритмически вычислимых и являющихся частично рекурсивными;
эквивалентность различных по форме уточнений понятий алгоритма.

На следующем шаге мы рассмотрим итерацию.

Предыдущий шаг Содержание Следующий шаг