На этом шаге мы рассмотрим связь между рекурсией и итерацией.
Рассмотрим подробнее связь между рекурсией и итерацией на примере ряда задач. Первый пример демонстрирует случай явного преимущества итерационного решения над рекурсивным - вычисление чисел Фибоначчи.
- Рекурсивный вариант.
function Fr (n: integer): integer; begin if n = 1 or n = 2 then Fr:= 1 else Fr:=Fr(n-l) + Fr(n-2); end;
- Итеративный вариант.
function Fi (n: integer): integer; var i, N1, N2, Result: integer ; begin N1:= 1; N2:= 1; {Установка начальных значений} Result:= 1; {на тот случай, если n = 1 или 2.} for i:= 3 to n do {Не выполняется, если n < 3.} begin Result:= N1 + N2; {Соответствует основной формуле чисел Фибоначчи.} N2:= N1; {Сдвиг значений на один индекс.} N1:= Result {Сдвиг значений на один индекс.} end; Fi:= Result {Установка значения функции.} end;
К сравнительной оценке этих двух алгоритмов можно подходить с двух позиций: использования ресурсов ЭВМ и сложности написания и отладки программы.
- Ресурсы. В данном случае под ресурсами понимается время процессора и объем занятой программой (и данными) памяти.
Рекурсивная программа включает следующие операции, занимающие время процессора: вызов функции, сравнение n с единицей и двойкой, сложение; при каждом вызове происходят сравнения и в части вызовов (если n>2) происходят сложения. Поэтому решающим параметром в оценке времени является количество вызовов функции. Все вызовы можно разбить на уровни следующим образом. На первом уровне находится единственный первый вызов с параметром n. На втором уровне находятся два вызова (с параметрами n-1 и n-2), произведенные при первом вызове. На третьем уровне находятся четыре вызова с параметрами n-2, n-3, n-3, n-4 и т. д. с увеличением количества на каждом уровне в два раза по отношению к предыдущему уровню до тех пор, пока величины n-i не начнут достигать значения 2. Эти вызовы можно изобразить в виде дерева (рисунок 1).
Здесь для определенности взято n-7. Непросто оценить, сколько вершин (вызовов) в этом дереве, но можно быстро получить неравенства, ограничивающие это количество сверху и снизу. Левая ветвь помечена числами n, n-1, n-2, n-3, ..., 2. Следовательно, количество уровней не превосходит величины n-1. Правая ветвь помечена числами n, n-2, n-4, n-6 = 1. Можно сделать вывод, что количество уровней не меньше n/2. Если дерево имеет k уровней, то в нем 1+2+4+8+...+2k-1=2k вершин или, учитывая неравенство n-1 > k > n/2, получаем 2n-1-1 > число вызовов > 2n/2.
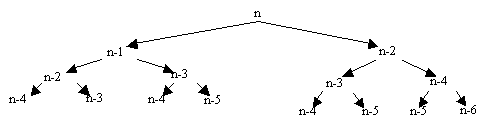
Рис.1. Дерево вызовов рекурсивной функции вычисления чисел ФибоначчиКак верхняя, так и нижняя границы быстро растут с увеличением n. Уже при n=20 требуется не менее 1000 вызовов, хотя, как это ясно видно из дерева, многие вызовы дублируют друг друга - текст функции не предусматривает контроля дублирования. С каждым незавершенным вызовом функции связано хранение в стеке определенных данных (это обсуждалось, когда рассматривался механизм реализации рекурсии). Ввиду того, что проход по дереву производится в глубину, в любой момент времени требуется хранить от n-1 до n/2 групп данных.
Итеративная программа включает сложения, пересылки (присваивания) и проверки (неявные) цикла на окончание. Занятость процессора в этом случае удобно оценить количеством исполнений тела цикла. Заголовок цикла ясно указывает на то, что тело цикла (одно сложение, три пересылки и команды управления циклом) выполняется n - 2 раза; кроме этого три пересылки (присваивания) в начале и одно в конце. Таким образом, количество операций может быть оценено формулой an+b. Количество использованной памяти - память для четырех переменных.
Эти расчеты показывают явное преимущество итеративного метода в сравнении с рекурсивным по использованию ресурсов ЭВМ для решения данной задачи.
- Сложность написания и отладки программы. По существу это вопрос о затратах труда программиста. Формальные числовые оценки здесь
затруднительны. Но сравнение двух текстов показывает, что рекурсивная программа пишется автоматически на основе постановки задачи, в то время как итеративная
требует преобразования задачи и "изобретения" алгоритма, введения дополнительных переменных, отсутствовавших в постановке задачи, и неочевидных операций.
Все это приводит к необходимости доказательства того, что полученный алгоритм действительно решает поставленную задачу, а не какую-то другую, что он правильно
работает для всех допустимых исходных данных. Положение осложняется тем, что вместо статического анализа текста (в случае рекурсии) необходимо представлять, как алгоритм
разворачивается во времени с помощью некоего исполнителя, т.е. привлекать модель компьютера.
С этой точки зрения рекурсивный алгоритм предпочтительнее итеративного.
Анализ пунктов (А) и (Б) дает нам противоречивые советы. В случае таких простых задач как вычисление чисел Фибоначчи вопрос обычно решается в пользу ресурсов компьютера.
Есть случаи, когда размышлять о выборе метода не приходится. Рекуррентная формула может быть предназначена для порождения неограниченной последовательности значений. Следующий алгоритм является примером как раз такой ситуации.
Задача о генерации псевдослучайных чисел. При решении некоторых задач требуется использовать случайные числа. Это задачи имитационного моделирования, кодирования сообщений, компьютерные игры и другие. Проблема программной генерации случайных чисел вступает в противоречие с одним из свойств алгоритмов - свойством детерминированности (определенности). Программа вычисляет значение функции некоторого аргумента и для одного и того же значения аргумента всегда получается одно и то же значение функции (под аргументом понимаем все исходные данные программы, в том числе и показания системного таймера, если он используется в программе, и др.). В большинстве приложений и не требуются истинные случайные числа (затрудняемся даже объяснить, что это такое), достаточно, чтобы полученная последовательность казалась случайной. В слово "казалась" обычно вкладывают следующий смысл.
Пусть x1, x2, x3, ..., xi, ..., xn - последовательность чисел (вещественных или целых, в зависимости от приложения), a<xi<b. Последовательность должна выдерживать статистические тесты, зависящие от того, какими свойствами должны обладать требуемые случайные числа. Например, если хотим иметь равномерно распределенные независимые случайные числа. Тогда сумма всех xi, отнесенная к n, должна приблизительно равняться (a+b)/2, взаимная корреляция значений xi, и хi+1 должна быть близка к нулю, на любые два различных участка одинаковой длины внутри интервала [a,b] должно попадать примерно одинаковое количество чисел xi.
Существует очень много исследований, посвященных разработке методов программной генерации псевдослучайных чисел (они все-таки не случайные). Обзор некоторых из них приведен в книге Д. Кнута "Искусство программирования для ЭВМ" (Т. 2). Наиболее часто используется метод, предложенный в 1948 г. американским математиком Д. Лемером и названный линейным конгруэнтным методом. Этот метод применяется в большинстве датчиков, встроенных в компиляторы языков программирования. В вычислительном отношении он очень прост:
xi+1 = (а*xi + с) mod m,
где a, c, m - целые положительные константы (c может быть равно 0).
Обычно в некоторый момент времени прикладной программе нужно только одно число, поэтому процедура генерации может быть записана так:
function RANDOM (x: integer): integer;
const
a = 25173;
с = 13849;
m = 65536;
begin
RANDOM:= (a*x +c) mod m;
end;
Первый раз функция вызывается с некоторым аргументом х0, например, 12345. Значение хi = RANDOM (x0) нужно запомнить в прикладной программе с тем, чтобы получить следующее число x2 = RANDOM (x1) и так далее. Константы a, c, m, x0, конечно, могут быть выбраны и не такими как в этом примере. Однако теория чисел и модулярная арифметика часто преподносят сюрпризы, поэтому, прежде чем выбрать a, c и m, нужно познакомиться с соответствующей теорией (см. книгу Д. Кнута).
В контексте сравнения рекурсивных и итерационных алгоритмов можно сказать, что эта задача чисто итерационная и попытки применять рекурсию для ее решения бессмысленны с любой (практической) точки зрения.
Второй пример рекурсивного и итеративного решений - вычисление биномиальных коэффициентов. Высота бинарного дерева вызовов (количество уровней) равна n, хотя и не все ветви достигают такой длины. Следовательно, общее количество вызовов не превышает величины 2k-1.
Получить итеративное решение использованием формулы разложения биномиального коэффициента в сумму двух более простых биномиальных коэффициентов, но в обратном порядке, как это было сделано для чисел Фибоначчи, затруднительно. Из-за зависимости коэффициентов от двух индексов их уже нельзя расположить в виде цепочки: здесь не будет одного или двух начальных значений. Началом будет вся крона дерева. Проще воспользоваться другими математическими соотношениями, более приспособленными к итеративной форме вычислений. В частности, известна формула:
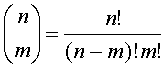
Ее можно использовать, не прибегая к вычислению факториалов. Пусть k - максимальное из двух значений: n-m и m, а l - минимальное. Тогда эта формула может быть сокращена:
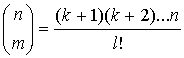
Она используется для непосредственного вычисления значения биномиальных коэффициентов:
function BC(n, m: integer): integer;
var
i, k, 1, p, q: integer;
begin
if n - m >= m then
begin
k := n - m;
l := m;
end
else
begin
k := m;
1 := n - m;
end;
P := 1; q := 1;
for i := k + 1 to n do
p := p * i;
for i := 2 to 1 do
q := q * i;
ВС := р div q;
end;
В этом варианте не вычисляется ничего дважды, в отличие от рекурсивного, и количество операций линейно зависит от n.
На следующем шаге мы рассмотрим реализацию механизма рекурсии.
