Шаг 18.
Понятие рекурсии.
Реализация механизма рекурсии

    На этом шаге мы рассмотрим реализацию механизма рекурсии.

    Исполнение рекурсивной процедуры (функции) оказывается для компьютера не совсем простой задачей. Для того чтобы поддержать все возможности, заложенные в схеме рекурсии, компьютер должен выполнить ряд действий, скрытых от программиста. Необходимость этих действий диктуется тем, что имеется определенный разрыв между алгоритмическим языком высокого уровня, освобождающим программиста от заботы о деталях организации вычислительного процесса, и машинным языком (типичного, не специализированного компьютера), в котором все детали должны быть учтены. Чем более "интеллектуальной" является конструкция языка высокого уровня, тем больше разрыв и тем больше скрытых действий должен выполнить компилятор языка по подготовке объектного кода.

    Чтобы более ясно представить себе то, что происходит на машинном уровне во время выполнения рекурсивных процедур (а, значит, решить, насколько возможно и эффективно их использование в том или ином случае), рассмотрим несколько примеров.

1. Выполнение оператора присваивания ... Z:= 2*а + b; ... для скалярных переменных в главной программе. Компилятор генерирует очевидные команды: умножение, сложение операндов и пересылка результата в область памяти, отведенную для переменной Z. Здесь нет скрытых действий за исключением, быть может, введения рабочих переменных, если выражение в правой части оператора присваивания достаточно сложное. Это определяется интенсивным использованием регистров в системах команд ЭВМ для ускорения операций.

2. Вычисление с вызовом функции. Дано определение функции:

       function Sum(X, Y: integer): integer;
       begin
         Sum:= X + Y;
       end;
   

       В вызывающей программе имеется обращение:

       begin 
         ...
         Z:= Sum(2*a, b);
         ...
       end.
   

       Компилятор сгенерирует команды, которые в вызывающей программе:

   • вычислят значения фактических параметров;
   • в специально отведенной области памяти вызывающей программы сформируют список параметров (как правило, непрерывный участок памяти, в который занесены адреса параметров);
   • запишут адрес списка параметров в один из регистров процессора (его номер оговаривается соглашениями);
   • выполнят переход к начальной команде функции Sum и передачу этой функции адреса возврата;
   • после возврата из функции перешлют полученный результат в область памяти, отведенную для переменной Z.

       В вызываемой программе (функции Sum):

   • обеспечивается сохранение содержимого регистров процессора в оперативном запоминающем устройстве;
   • значения фактических (входных) параметров, взятые из списка, переписываются в память формальных параметров X и Y;
   • производятся вычисления в соответствии с операторами тела функции;
   • восстанавливается содержимое регистров процессора;
   • выполняется команда возврата в вызывающую программу.

       Из приведенного перечня видно, что использование процедур и функций требует дополнительных действий. Каждая процедура имеет контекст, в котором она выполняется. Упрощенно говоря, это набор данных, связанных с процедурой, и их значений; в частности - локальные переменные и формальные параметры. При входе в вызываемую процедуру контекст создается, а при возврате в вызывающую программу ее контекст должен восстанавливаться.

       При компиляции процедуры необходимо решить один важный вопрос: как быть с ее локальными переменными и параметрами, передаваемыми по значению (роль которых внутри процедуры такова же, как и роль локальных переменных)?

       С точки зрения языка они не существуют, пока процедура не активизирована (вызвана); и перестают существовать после завершения процедуры. Это означает, что можно выделять для них память в момент активизации и отдавать ее обратно системе по завершении выполнения процедуры. Но если вызовы процедуры находятся в цикле, действия по работе с памятью могут значительно увеличить суммарное время работы программы, производятся ли запросы в отношении выделения памяти к операционной системе или память берется из специальной области - стека.

       Повышения скорости вычислений можно добиться, если назначить локальным переменным адреса (относительные) при компиляции. Тогда область памяти будет закреплена за ними в течение всего времени выполнения программы и команды в процедуре можно сгенерировать с учетом известных адресов. При этом, правда, несколько уменьшается эффективность использования памяти, но если в процедуре нет больших локальных массивов, то на это можно пойти.

       Опасность такого подхода не в неэффективном использовании памяти. Она гораздо серьезнее! Представим себе, что работа происходит в среде многопрограммной операционной системы и/или на многопроцессорной вычислительной системе и функция Sum вызвана почти одновременно двумя программами (с разными, разумеется, фактическими параметрами). Точнее говоря, вторая программа вызвала функцию Sum после того, как это сделала первая, но до того как завершился первый вызов. Программный код - ресурс не расходуемый (если нет вирусов), поэтому два процессора вполне могут поделить команды кода, считывая из памяти один и тот же участок кода, каждый в свой кэш команд или другим способом. Дело в том, что команды не зависят от фактических параметров функции. Но значения локальных переменных зависят! Если локальная память функции уже используется первым вызовом (т.е. первой программой), то начало работы второго вызова разрушит значения в поле локальных данных. В результате оба вызова будут мешать друг другу, перечеркивая то, что было только что записано соперничающим вызовом, и ни первая, ни вторая программы не получат ожидаемых результатов.

       Процедуры и функции, которые обеспечивают правильную работу в такой ситуации, т.е. возможность вновь вызвать процедуру ("войти" в процедуру), хотя еще не завершились предыдущие вызовы, называются реентерабельными (повторновходимыми). Для обеспечения реентерабельности нужно память локальных переменных связывать не с процедурой, а с каждым вызовом процедуры.

3. Аналогичная проблема возникает при реализации рекурсивных процедур, даже если они выполняются на однопроцессорной вычислительной системе в среде однопрограммной ОС. Как следует из текста рекурсивной процедуры, она обращается к самой себе, т.е. генерирует новый вызов до завершения предыдущего. Но эта проблема одновременно и сложнее и проще предыдущей.

       Сложнее потому, что глубина вложения (глубина рекурсии) может быть очень большой, как показывает хотя бы случай вычисления факториала:

       function FACTORIAL( N: integer ): integer;
       begin 
         if N = 1 then FACTORIAL:= 1
         else FACTORIAL:= N * FACTORIAL (N -1) 
       end;
       :
       begin 
          ... {Фрагмент вызывающей программы.}
         K:= FACTORIAL(M); {Этот вызов порождает еще М-1 вызовов. }
          ...
       end.
   

       Нерекурсивная процедура разными программами в многопрограммной ОС может быть одновременно вызвана лишь с изрядной долей случая.

       Но старты и завершения разных вызовов процедуры в многопрограммной или многопроцессорной системе никак не синхронизированы: более ранний вызов может закончиться и раньше и позже более позднего. Это зависит как от различий в фактических параметрах вызовов (исполнение пойдет по разным ветвям в процедуре), так и от различий в скорости процессоров или из-за особенностей в дисциплине предоставления квантов времени процессора в однопроцессорной многопрограммной системе. Асинхронность несколько осложняет управление памятью. В то же время при вызовах рекурсивных процедур соблюдается четкий порядок.

       Более ранний рекурсивный вызов всегда закончится позже. Этот факт позволяет применить для управления локальной памятью рекурсивных процедур такую структуру данных как стек. Стек характеризуется следующими свойствами: он имеет неопределенный размер (реально размер ограничен техническими параметрами компьютера); элементы стека не нумеруются, доступен (для чтения) только один элемент, верхний; после удаления из стека верхнего элемента доступным становится следующий и т.д.; вновь помещаемый в стек элемент становится верхним. Таким образом, стек - линейная структура данных, доступная для чтения и записи только с одного конца, т.е. работа со стеком подчиняется дисциплине LIFO (last in - first out, последним включен - первым удален). Стек можно моделировать линейным списком, но это неэффективно по времени, поэтому обычно стек моделируется одномерным массивом и двумя индексными переменными - указателями на дно и на вершину стека. Современные компьютеры поддерживают стеки аппаратно - специальными регистрами-указателями на сегменты памяти, предназначенные для размещения стеков, на вершины стеков и командами для выполнения операций со стеками.

       Работа со стеком производится следующим образом. При первом вызове рекурсивной процедуры (функции) в стеке резервируется место для всех значений, связанных с этим вызовом (это могут быть не только локальные переменные и параметры, но и некоторая служебная информация, скрытая от программиста). Делается это простым изменением значения указателя на вершину стека: оно увеличивается на необходимое число байт, если стек растет в сторону старших адресов памяти, или (как во многих компьютерах) уменьшается, если стек растет в сторону младших адресов памяти.

       Перед вторым вызовом в области памяти первого вызова будут находиться некоторые значения, соответствующие начатым, но не завершенным вычислениям. Второй вызов резервирует в стеке область над областью первого вызова тем самым, перекрывая к ней доступ.

   
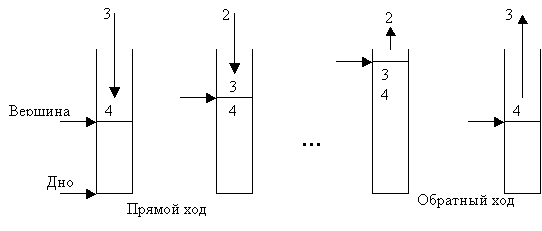
   Рис.1. Изменение содержимого стека при обработке рекурсивных вызовов

       Таким образом, вплоть до последнего вызова стек будет заполняться (так называемый прямой ход рекурсии). На рисунке 1 показаны состояния стека при выполнении вызова Factorial (4); нижняя область между дном и вершиной уже использована ранее вызванными другими процедурами (вызывающими по отношению к функции Factorial). Первый вызов помещает в стек значение 4, второй 3 и т.д. до тех пор, пока фактическим параметром вызова не станет значение 1. Затем начинается серия завершений вызовов с извлечением из стека сохраненных значений и использованием их для продолжения вычислений (в данном примере для выполнения операции умножения). Последним завершается первый вызов. На рисунке 1 изображено смещение указателя на вершину области.

Предыдущий шаг Содержание