На этом шаге мы рассмотрим осбые случаи анализа сложности рекурсивных алгоритмов.

    Если функция f(Х) преобразования аргумента при рекурсивном вызове нелинейна, то аналитическое отыскание функции сложности алгоритма редко бывает возможно. Общих методов в этом случае нет, и приходится привлекать сведения из соответствующей проблемной области, а не только информацию о структуре программы. Аналогичная ситуация имеет место и для итеративных алгоритмов при оценке числа выполнений тела цикла while или repeat. Интересным примером такого рода является алгоритм Евклида отыскания наибольшего общего делителя. Напомним его текст.

  function GCD (n, m: integer): integer; 
  begin 
    if m = 0 then GCD := n
    else GCD := GCD (m, n mod m);
  end;

    Здесь функция f(X) = f(n,m) = (m,n mod m) переставляет второй аргумент на место первого, а на место второго аргумента ставит значение f(n,m). Это нелинейное преобразование.

    Оценим сверху количество рекурсивных вызовов функции GCD. Для этого выпишем последовательно соотношения, определяющие аргумент X. Предположим для определенности, что n > m (при обратном неравенстве первый вызов функции просто меняет аргументы местами, а при равенстве n = m процесс завершается за один шаг). В качестве параметра V сложности исходных данных целесообразно принять меньший из аргументов функции, т.е. V = m, так как именно с него начинаются операции деления (нахождения модулей) - если увеличить m на произвольно большое число, кратное m (например, m*10¹⁰⁰⁰), то это не изменит количества шагов. Следовательно, max(n,m) не является хорошим аргументом функции сложности.

    При рекурсивных вызовах вычисляются остатки от деления, которые мы обозначим R_i: R_i=R_(i-2) mod R_(i-1). Начало процесса определяется значениями R₀ = n, R₁ = m. Иначе остатки можно определить системой равенств:

  R0 = R1d1 + R2,
  R1 = R2d2 + R3,
  R2 = R3d3 + R4,
  . . . . .
  Rk-2 = Rk-1dk-1 + Rk,
  Rk-1 = Rkdk

где d_i - частные от деления. Процесс завершается, когда очередной остаток от деления будет равен нулю. Очевидно, что процесс будет наиболее длительным, если все d_i = 1. Перенумеруем последовательность остатков с конца:

  Rk+1 = 0 = F0,
  Rk = F1,
  Rk-1 = F2,
  . . . . .
  Rk-i+1 = Fi,
  R1 = Fk.

    Тогда предыдущую систему при условии d_i = 1 можно записать в виде одного рекуррентного уравнения

  Fi = F(i-1) + F(i-2)

при начальных условиях F₀ = 0, F₁ = F₂ и условии на конце: F_k равно m или ближайшему к m снизу числу, удовлетворяющему рекуррентному уравнению. Заметим, что не требуем, чтобы F_(k+l) = m, так как это требование может (но не всегда) войти в противоречие с условиями d_i=1. Последовательность F_i пока еще не определена однозначно - не хватает начального условия - значения F₁. Это значение мы выберем так, чтобы последовательность имела максимальную длину (при условии F_k = m). Очевидно, это должно быть минимальное ненулевое значение, т. е. F₁ = 1.

    Становится ясно, что последовательность {F_i} - это последовательность чисел Фибоначчи. Теперь задача получения верхней оценки сложности алгоритма Евклида сводится к следующему: найти номер k максимального из чисел Фибоначчи F_k <= m.

    Величина k и является оценкой сложности алгоритма.

    Из теории чисел Фибоначчи известно, что F_k может быть выражено формулой

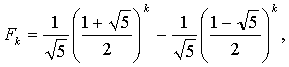
число

известно как золотое сечение, φ= 1,618. Поскольку второе слагаемое в формуле для F_k не превышает по абсолютной величине единицы, то можно написать следующие неравенства:

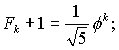
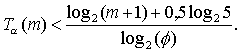
    Вывод средней оценки сложности алгоритма Евклида приведен в книге Д. Кнута (Т. 2, разд. 4.5.3). Однако, когда оценка худшего случая всего лишь логарифмическая, средняя оценка представляет, в основном, теоретический интерес (в данном случае она тоже логарифмическая, но с меньшим коэффициентом).

    С точки зрения анализа, как худшего, так и среднего, случаев интересна теорема Э.Чезаро: пусть q_N - число упорядоченных пар целых чисел (n, m), таких, что 1 <= n, m <= N и НОД(n,m) = 1. Тогда:

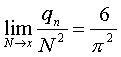
    Она говорит о том, что в 60% случаев алгоритм Евклида будет заканчиваться получением остатка, равного 1; такой остаток мы рассматривали как худший случай при анализе сложности.

    Замечание о золотом сечении. Определенное выше число φ, называемое золотым сечением и приблизительно равное 34/21, имеет довольно богатую историю. Помимо того, что оно возникает при решении чисто математических задач, им интересуются искусствоведы и психологи. В книге "Введение в эстетику" немецкий ученый Г. Т. Фехнер приводит следующие данные. Для изучения предпочтений по отношению к форме было взято десять прямоугольных карточек из белого картона, равных по площади квадрату со стороной 8 см, но с различными соотношениями сторон. Наименьшее отношение сторон соответствует квадратной карточке и равно 1:1, наибольшее - 5:2. Между этими крайними значениями имеется золотое сечение с отношением сторон 34:21. Различным людям ставился вопрос: какие из прямоугольников при максимальном абстрагировании от их возможного применения являются наиболее, а какие - наименее привлекательными? Более трети предпочли "золотое сечение", три близких отношения 34:21, 3:2, 23:13 предпочли в сумме около 73% опрошенных, никто не назвал золотое сечение наименее привлекательным. Более подробно об этом можно прочесть в книге "Семиотика и искусствометрия" (М: Мир, 1972).

    На следующем шаге мы рассмотрим сложность операций с бинарными деревьями.

Предыдущий шаг Содержание Следующий шаг