На этом шаге мы рассмотрим сложность операций с бинарными деревьями.
Бинарные деревья часто используются для хранения информации. Они выгодно отличаются от массивов фиксированного размера своим динамическим характером, возможностью почти неограниченно увеличивать объемы хранимой информации. От линейных списков их отличают лучшие временные характеристики - например, при поиске элемента (наиболее часто используемой операции) требуется в среднем просмотреть меньшую часть дерева, чем это требовалось бы для списка с таким же количеством элементов. Проведем детальный анализ функций сложности этих операций.
Прежде всего определим, какой параметр можно рассматривать в качестве параметра V сложности данных. Наиболее очевидным кандидатом на эту роль является текущее количество n вершин в дереве. Но ясно, что величина n не определяет однозначно сложность. Есть хорошие и плохие деревья. Оценим с этой точки зрения параметр n - насколько при одном и том же значении n для разных деревьев могут отличаться функции сложности одной из самых простых операций - вставки нового элемента.
Условия анализа будут следующими: включаемый элемент является новым, т. е. элемента с таким значением информационного поля еще нет в дереве; рассматриваются два вида деревьев - идеальное, имеющее n = 2k-1 вершин, и вырожденное (линейный список).
1. Идеальное дерево. В этом дереве все вершины располагаются на k уровнях: корень на первом уровне, две вершины на втором уровне, четыре вершины на третьем уровне, ..., 2k-1 вершины на k уровне. Новая вершина может быть помещена только на (k+1)-й уровень, для этого нужно определить, к какой ветви вершина будет подсоединена. Проверка начинается с корня. Сравнение информационных полей корня и новой вершины отвечает на вопрос, в каком поддереве, левом или правом, должна быть размещена новая вершина. После сравнения следует переход по ветви к корню соответствующего поддерева или, если ветвь уже закончилась, размещение новой вершины в конце ветви. Поскольку все ветви в идеальном дереве имеют одинаковую длину (содержат k вершин), то, считая элементарным шагом действие "сравнить информационные поля вершин и, либо перейти по ссылке к следующей вершине, либо разместить новую вершину", можно оценить сложность вставки величиной k =log2(n+1). Причем эта оценка одновременно является и максимальной и средней, она также не зависит от значения информационного поля нового элемента. 2. Вырожденное дерево. Это дерево представляет собой линейный список элементов, упорядоченных по возрастанию или убыванию значений информационных полей. Длина списка равна n и количество элементарных шагов (таких же, как и для идеального дерева) зависит на этот раз от включаемого элемента. Для определенности рассмотрим дерево, состоящее только из правых поддеревьев (в дерево включались упорядоченные по возрастанию элементы). Различаются три случая:
- новый элемент предшествует уже имеющимся, т. е. значение его информационного поля меньше значений информационных полей имеющихся в дереве вершин, в том числе корня; тогда новый элемент становится левым потомком корня, операция заканчивается за один шаг, дерево перестает быть вырожденным;
- все имеющиеся в дереве элементы предшествуют новому; новый элемент должен стать правым потомком последней (самой правой) вершины, для этого требуется выполнить n элементарных шагов; дерево остается вырожденным;
- новый элемент предшествует части вершин дерева, но другая часть вершин предшествует ему; в этом случае в списке имеется i-я вершина, левым потомком которой становится новый элемент; требуется выполнить i, 1<=i<=n, элементарных шагов, дерево перестает быть вырожденным.
В случае (в) максимальная оценка сложности равна n, а средняя зависит от того, каким является множество, из которого выбираются значения информационных полей элементов, какое распределение имеет выборка из n значений, уже помещенных в дерево, и каково вероятностное распределение, из которого было выбрано значение информационного поля нового элемента. За неимением подробных сведений об этом обычно берут среднюю оценку в виде (n+1)/2.
Таким образом, получаем оценки от log2(n+1) для лучших деревьев до n для худших деревьев при одинаковом количестве вершин n. Ясно, что максимальная оценка сложности включения элемента в произвольное дерево определяется худшим случаем. Со средней оценкой дело обстоит иначе. Усреднение должно быть произведено не только по характеристикам вновь включаемого элемента (как в случае "в"), но и по всевозможным деревьям. Поэтому следующим этапом является анализ того, как часто встречаются хорошие и плохие деревья.
Напомним, что если имеется идеальное дерево с n = 2k-1 вершинами, где k - количество уровней, то для присоединения к этому дереву нового элемента потребуется в точности k элементарных шагов (сравнений и переходов по указателю). Сколько потребуется элементарных шагов для отыскания элемента в идеальном дереве? Ответ на этот вопрос зависит от того, какие вершины к настоящему моменту имеются в дереве (каковы значения их информационных полей), и какую информацию мы ищем. Обычно, раздельно рассматривают 2 случая:
- информационное поле искомого элемента имеет значение, заведомо отсутствующее в дереве, так называемый неудачный поиск;
- искомый элемент присутствует в дереве, так называемый удачный поиск.
В первом случае количество сравнений такое же, как и при включении нового элемента, т. е. k, а количество переходов на единицу меньше.
Второй случай требует более подробного анализа. Предположим, что искомая вершина с равной вероятностью находится в любой из позиций идеального дерева. Время ее поиска однозначно определяется номером уровня, на котором эта вершина находится. Если это 1-й уровень (корень), то достаточно одного сравнения, если k-й уровень (одна из висячих вершин), то требуется максимальное количество сравнений - k. Таким образом, количество сравнений сn является случайной величиной, принимающей значения из интервала [1, k]. Осталось выяснить, какова вероятность pi, того, что сn примет значение i.
Очевидно, что, приняв условие равновероятности вершин при поиске, необходимо сделать вывод: вероятность попадания на некоторый уровень пропорциональна количеству вершин на этом уровне. Поскольку на каком-то из уровней искомая вершина обязательно находится, т. е. сумма вероятностей равна единице, то вероятность нахождения искомой вершины на i-м уровне равна отношению количества вершин i-го уровня к общему количеству вершин дерева:
![]()
Среднее количество сравнений (математическое ожидание) равно:
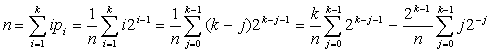
Первое слагаемое равно k, а для вычисления второго слагаемого можно использовать известную формулу:
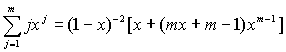
Таким образом, после преобразований получаем выражение:
![]()
Так как нас интересуют достаточно грубые оценки, то при больших k мы можем считать значение дроби приблизительно равным единице. Тогда n = k-1. Следовательно, максимальная и средняя сложность поиска информации в идеальном дереве почти совпадают.
Поскольку различие в сложности включения нового элемента в идеальное дерево и в дерево вырожденное значительно отличаются, а заранее не известно, какие деревья у нас будут получаться, то интересно найти ответы на следующие вопросы.
- Сколько существует различных бинарных деревьев с n вершинами?
- Сколько среди них вырожденных и как часто они возникают?
- Сколько среди деревьев идеальных или близких к идеальным, какие последовательности значений их порождают?
Ответы на эти вопросы важны потому, что если большинство деревьев - вырожденные, то деревья почти не имеют преимуществ перед списками, а недостаток очевиден - для деревьев требуется больше памяти. Если же большинство деревьев близки к идеальным, то дерево как структура данных для хранения информации имеет большое значение и стоит приложить усилия к совершенствованию процедур работы с деревьями (например, чтобы совсем исключить появление вырожденных деревьев).
На следующем шаге мы рассмотрим число бинарных деревьев.
