На этом шаге мы рассмотрим последний пример с использованием технологии CUDA.

    Напомним последовательный алгоритм (алгоритм Флойда) для поиска всех кратчайших путей графа.

    Ключевая идея алгоритма - разбиение процесса поиска кратчайших путей на фазы.

    Перед k-ой фазой величина d[i][j] равна длине кратчайшего пути из вершины i в вершину j, если этому пути разрешается заходить только в вершины с номерами, меньшими k (начало и конец пути не считаются). Заметим, что перед первой фазой матрица d[i][j] содержит исходную матрицу смежности. Если в графе не существует ребра из i в j, то в d[i][j] нужно записать "бесконечность" - число, которое будет больше возможного расстояния между этими вершинами. Для значений, стоящих на главной диагонали матрицы d[i][j] следует записать 0.

    На k-ой фазе нужно производить пересчет матрицы d[i][j] следующим образом. Зафиксируем вершины i и j. Тогда кратчайший путь между вершинами i и j либо уже найден, т.е. проходит только через вершины с номерами от 1 до k-1 и тогда значение d[i][j] следует оставить без изменения, либо кратчайший путь будет проходить через вершинку k. В этом случае значение d[i][j] нужно обновить значением d[i][k] + d[k][j].

    Из вышесказанного следует простая формула для подсчета всех d[i][j]:

  d[i][j] = min(d[i][j], d[i][k] + d[k][j]);

    Приведем ниже реализацию данного алгоритма в технологии CUDA.

1. Выделение памяти.

   int dev_n = n * n * sizeof(double);
   double *dev_Matrix;
   cudaMalloc((void**) &dev_Matrix, dev_n);
   

2. Копирование данных из памяти CPU в память GPU.

   cudaMemcpy(dev_Matrix, Matrix, dev_n, cudaMemcpyHostToDevice);
   

3. Осуществление запуска ядер-функций.

   dim3 threads(BLOCKSIZE, BLOCKSIZE);
   dim3 grid(n/BLOCKSIZE, n/BLOCKSIZE);
   for(int k = 0; k < n; ++k) {
    Kernel<<<grid, threads>>>(dev_Matrix, k, n);
   }
   

       Для того, чтобы ядро посчитало все кратчайшие пути, его нужно запускать для каждой вершины графа.

4. Копирование результатов из памяти GPU в память CPU.

   cudaMemcpy(Matrix, dev_Matrix, dev_n, cudaMemcpyDeviceToHost);
   

5. Освобождение памяти в GPU.

   cudaFree(dev_Matrix);
   cudaDeviceReset();
   

    Ниже приведем реализацию ядра.

const int BLOCKSIZE = 16;
const double INF = 1e9;

void __global__ Kernel(double *Matrix, int k, int n){
 int i = blockIdx.y * BLOCKSIZE + threadIdx.y;
 int j = blockIdx.x * BLOCKSIZE + threadIdx.x;

 if (i < n && j < n && Matrix[i*n + k] < INF && Matrix[k*n + j] < INF){
  Matrix[i*n+j] = min(Matrix[i*n + j], Matrix[i*n + k] + Matrix[k*n + j]);
 }
}

    Весь проект можно взять здесь.

    Приведем ниже результаты времени выполнения созданных приложений.

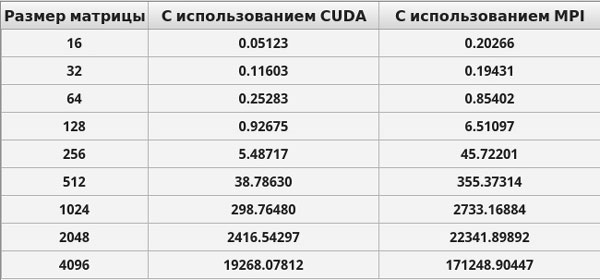
Рис. 1. Результаты нахождения всех кратчайших расстояний в графе на персональном комьютере (время выполнения приведено в милисекундах)

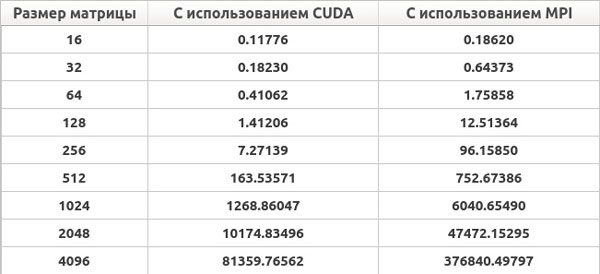
Рис. 2. Результаты нахождения всех кратчайших расстояний в графе на ноутбуке (время выполнения приведено в милисекундах)

    На следующем шаге мы подведем некоторые итоги.

Предыдущий шаг Содержание Следующий шаг