Шаг 28.
Технология CUDA.
Пример 3. Решение систем линейных алгебраических уравнений

    На этом шаге мы рассмотрим третий пример с использованием технологии CUDA.

    Напомним алгоритм Гаусса.

    Алгоритм Гаусса состоит из двух шагов:

1. Прямой ход - приведение матрицы коэффициентов к треугольному виду, т.е. к матрице в которой все элементы, стоящие ниже главной диагонали равны 0, а элементы главной диагонали равны 1.
2. Обратный ход - приведение треугольной матрицы к единичной матрице.

    Для простоты будем считать, что в данной системе количество уравнений совпадает с количеством неизвестных.

    Приведем ниже реализацию данного алгоритма с помощью технологии CUDA.

1. Выделение памяти.

   double *dev_a, *dev_b;
   cudaMalloc((void **) &dev_a, n * n * sizeof(double));
   cudaMalloc((void **) &dev_b, n * sizeof(double));
   

2. Копирование данных из памяти CPU в память GPU.

   cudaMemcpy(dev_a, h_A, n * n * sizeof(double), cudaMemcpyHostToDevice);
   cudaMemcpy(dev_b, h_B, n * sizeof(double), cudaMemcpyHostToDevice);
   

3. Осуществление запуска ядер - функций.

   dim3 Grid(n/BlockSize, n/BlockSize);
   dim3 Block(BlockSize, BlockSize);
   for(int i = 0; i < n - 1; ++i) 
      kernel_down<<<Grid, Block>>>(dev_a, dev_b, n, i, i);
   for(int i = n - 1; i >= 0; --i) 
      kernel_up<<<Grid,Block>>>(dev_a, dev_b, n, i, i);
   

       В данном примере мы используем уже два ядра. Одно для организации прямого хода (kernel_down), другое для организации обратного хода (kernel_up).

       При каждом вызове ядра kernel_down все элементы i-ого столбца матрицы dev_a, стоящие ниже i-ой строки обнуляются. Остальные элементы изменяются, согласно алгоритму Гаусса.

       Аналогично, при каждом вызове ядра kernel_up все элементы матрицы, стоящие в i-ом столбце и выше строки i изменятся на 0.

4. Копирование результатов из памяти GPU в память CPU.

   cudaMemcpy(h_A, dev_a, n*n*sizeof(double), cudaMemcpyDeviceToHost);
   cudaMemcpy(h_B, dev_b, n*sizeof(double), cudaMemcpyDeviceToHost);
   

       Заметим, что в данной реализации мы не получаем единичную матрицу с помощью ядра kernel_down, т.к. это выгоднее произвести на CPU после завершения ядра kernel_up. Сделать это можно с помощью следующего фрагмента кода:

   for(int i = 0; i < n - 1; ++i) h_C[i] = h_B[i]/h_A[i*n + i];
   

5. Освобождение памяти в GPU.

   cudaFree(dev_a);
   cudaFree(dev_b);
   cudaDeviceReset();
   

    Ниже приведем реализацию ядер.

1. Прямой ход.

   __global__ void kernel_down(double *A, double *B, int n, 
                                int number_row, int number_column){
    int bx = blockIdx.x;
    int by = blockIdx.y;
    int tx = threadIdx.x;
    int ty = threadIdx.y;
    int row = by*BlockSize + ty;
    int column = bx*BlockSize + tx;
   
    if(number_column < column && number_row < row){
     double glav = A[row*n + number_column]/A[number_row*n + number_column];
   
     if(number_column == column) B[row] -= B[number_row]*glav;
     A[row*n + column] -= glav*A[number_row*n + column];
    }
   }
   

2. Обратный ход.

   __global__ void kernel_up(double *A, double *B, int n, 
                                int number_row, int number_column){
    int bx = blockIdx.x;
    int by = blockIdx.y;
    int tx = threadIdx.x;
    int ty = threadIdx.y;
    int row = by*BlockSize + ty;
    int column = bx*BlockSize + tx;
   
    if(number_column == column && number_row > row){
     double glav = A[row*n + number_column]/A[number_row*n + number_column];
   
     B[row] -= B[number_row]*glav;
     A[row*n + column] = 0;
    }
   }
   

    Весь проект можно взять здесь.

    Приведем ниже результаты времени выполнения созданных приложений.

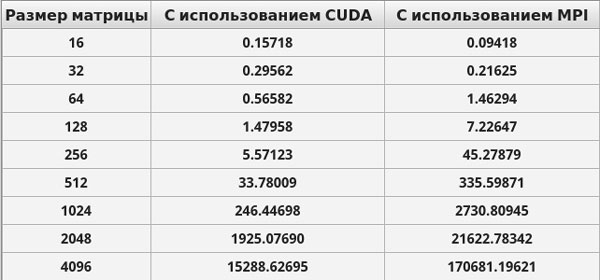
Рис. 1. Результаты решения систем линейных алгебраических уравнений на персональном комьютере (время выполнения приведено в милисекундах)

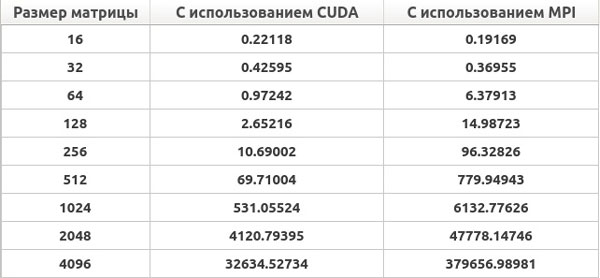
Рис. 2. Результаты решения систем линейных алгебраических уравнений на ноутбуке (время выполнения приведено в милисекундах)

    На следующем шаге мы рассмотрим последний пример с использованием технологии CUDA.

Предыдущий шаг Содержание Следующий шаг