На этом шаге мы рассмотрим cогласованность матриц сравнений.

В предыдущем примере шага 55 мы отмечали, что все столбцы нормализованных матриц N и N_R идентичны, а столбцы матрицы N_L таковыми не являются. Одинаковые столбцы указывают на то, что результирующие относительные веса сохраняют одно и то же значение независимо от того, как выполняется сравнение. В этом случае говорят, что исходные матрицы сравнения А и A_R, являются согласованными. Следовательно, матрица A_L не является таковой.

Согласованность означает, что решение будет согласовано с определениями парных сравнений критериев или альтернатив. С математической точки зрения согласованность матрицы А означает, что a_ija_jk = a_ik для всех i, j и k. Например, в матрице A_R из примера шага 55 a₁₃ = 3 и a₁₂a₂₃ = 3. Свойство согласованности требует линейной зависимости столбцов (и строк) матрицы А. В частности, столбцы любой матрицы сравнений размерностью 2x2 являются зависимыми, и, следовательно, такая матрица всегда является согласованной.

Не все матрицы сравнений являются согласованными. Действительно, принимая во внимание, что такие матрицы строятся на основе человеческих суждений, можно ожидать некоторую степень несогласованности.

Чтобы выяснить, является ли уровень согласованности "допустимым", необходимо определить соответствующую количественную меру для матрицы сравнений А. В примере шага 55 мы видели, что идеально согласованная матрица А порождает нормализованную матрицу N, в которой все столбцы одинаковы:

Отсюда следует, что матрица сравнений А может быть получена из матрицы N путем деления элементов i-го столбца на w_i (это процесс, обратный к нахождению матрицы N из А). Итак, получаем следующее.

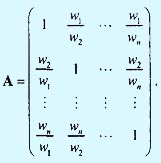
Используя приведенное определение матрицы А, имеем

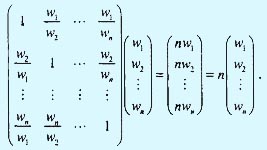
В компактной форме условие согласованности матрицы А формулируется следующим образом. Матрица А будет согласованной тогда и только тогда, когда

где w — вектор-столбец относительных весов w_i, i = 1, 2, ..., n. Когда матрица А не является согласованной, относительный вес w_i аппроксимируется средним значением n элементов i-й строки нормализованной матрицы N (см. пример шага 55). Обозначив через w вычисленную оценку (среднее значение), можно показать, что

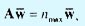
где n_max ≥ n. В этом случае, чем ближе n_max к n, тем более согласованной является матрица сравнения А. В результате в соответствии с методом анализа иерархий вычисляется коэффициент согласованности в виде

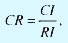
где

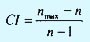- коэффициент согласованности матрицы А,

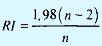- стохастический коэффициент согласованности матрицы А.

Стохастический коэффициент согласованности RI определяется эмпирическим путем как среднее значение коэффициента CI для большой выборки генерированных случайным образом матриц сравнения А.

Коэффициент согласованности CR используется для проверки согласованности матрицы сравнения А следующим образом. Если CR < 0,1, уровень несогласованности является приемлемым. В противном случае уровень несогласованности матрицы сравнения А является высоким, и лицу, принимающему решение, рекомендуется проверить элементы парного сравнения a_ij матрицы А в целях получения более согласованной матрицы.

Значение n_max вычисляется на основе матричного уравнения 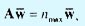при этом нетрудно заметить, что i-e уравнение этой системы имеет вид:

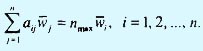
Поскольку 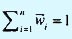легко проверить, что

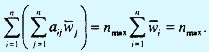
Это значит, что величину n_max можно определить путем вычисления вектор-столбца Aw с последующим суммированием его элементов.

На следующем шаге мы рассмотрим пример исследования согласованности матриц.

Предыдущий шаг Содержание Следующий шаг