На этом шаге мы рассмотрим способы определения весовых коэффициентов.
Сложность метода анализа иерархий заключается в определении относительных весовых коэффициентов (таких, как использованные в примере шага 53) для оценки альтернативных решений. Если имеется n критериев на заданном уровне иерархии, соответствующая процедура создает матрицу А размерности n, именуемую матрицей парных сравнений, которая отражает суждение лица, принимающего решение, относительно важности разных критериев. Парное сравнение выполняется таким образом, что критерий в строке i (i = 1, 2, ..., n) оценивается относительно каждого из критериев, представленных n столбцами.
Обозначим через aij элемент матрицы А, находящийся на пересечении i-й строки и j-го столбца. В соответствии с методом анализа иерархий для описания упомянутых оценок используются целые числа от 1 до 9. При этом: aij = 1 означает, что i-й и j-й критерии одинаково важны, aij = 5 отражает мнение, что i-й критерий значительно важнее, чем j-й, aij = 9 указывает, что i-й критерий чрезвычайно важнее j-го.
Другие промежуточные значения между 1 и 9 интерпретируются аналогично. Согласованность таких обозначений обеспечивается следующим условием: если aij = k, то автоматически aij = 1/k.
Кроме того, все диагональные элементы aij матрицы А должны быть равны 1, так как они выражают оценку критериев относительно самих себя.
Пример. Покажем, как определяется матрица сравнения А для задачи выбора Мартина из примера шага 53. Начнем с главного иерархического уровня, который имеет дело с критериями академической репутации университета и его местонахождения. С точки зрения Мартина, академическая репутация университета значительно важнее его местонахождения. Следовательно, он приписывает элементу (2, 1) матрицы А значение 5, т.е. a21 = 5. Это автоматически предполагает, что a12 = 1/5. Обозначив через R и L критерии репутации университета и его местонахождения, можно записать матрицу сравнения следующим образом.
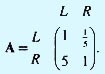
Относительные веса критериев R и L могут быть определены путем деления элементов каждого столбца на сумму элементов этого же столбца. Следовательно, для нормализации матрицы А делим элементы первого столбца на величину 1 + 5 = 6, элементы второго — на величину 1 + 1/5 = 1,2. Искомые относительные веса wR и wL критериев вычисляются теперь в виде средних значений элементов соответствующих строк нормализованной матрицы А. Следовательно,
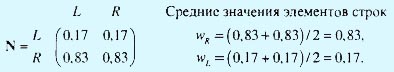
В результате вычислений получили wR = 0,83 и wL = 0,17. Столбцы матрицы N одинаковы, что имеет место лишь в случае, когда лицо, принимающее решение, проявляет идеальную согласованность в определении элементов матрицы А. Относительные веса альтернативных решений, соответствующих университетам А, В и С, вычисляются в пределах каждого критерия R и L с использованием следующих двух матриц сравнения.

Элементы матриц АR и АL определены на основе суждений Мартина, касающихся относительной важности трех университетов. При делении элементов каждого столбца матриц АR и АL на сумму элементов этих же столбцов получаем следующие нормализованные матрицы.

Величины (wRA, wRB, wRC) = (0,545, 0,273, 0,182) дают соответствующие веса для университетов А, В и С с точки зрения академической репутации.
Аналогично величины (wLA, wLB, wLC) = (0,129, 0,277, 0,594) являются относительными весами, касающимися местонахождения университетов.
На следующем шаге мы рассмотрим согласованность матриц сравнений.
