На этом шаге мы рассмотрим критерий ожидаемого значения и дерево решений.
Критерий ожидаемого значения сводится либо к максимизации ожидаемой (средней) прибыли, либо к минимизации ожидаемых затрат. В данном случае предполагается, что прибыль (затраты), связанная с каждым альтернативным решением, является случайной величиной.
Дерево решений
В приведенном ниже примере рассматривается простая ситуация, связанная с принятием решения при наличии конечного числа альтернатив и точных значений матрицы доходов.
Пример. Предположим, что вы хотите вложить на фондовой бирже 10 000 долл. в акции одной из двух компаний: А или B. Акции компании А являются рискованными, но могут принести 50 % прибыли от суммы инвестиции на протяжении следующего года. Если условия фондовой биржи будут неблагоприятны, сумма инвестиции может обесцениться на 20 %. Компания B обеспечивает безопасность инвестиций с 15 % прибыли в условиях повышения котировок на бирже и только 5 % — в условиях понижения котировок. Все аналитические публикации, с которыми можно познакомиться (а они всегда есть в изобилии в конце года), с вероятностью 60 % прогнозируют повышение котировок и с вероятностью 40 % — понижение котировок. В какую компанию следует вложить деньги?
| Альтернативные решения | Прибыль за один год от инвестиций 10000 долл. | ||
| При повышении котировок (долл.) | При понижении котировок (долл.) | ||
| Акции компании А | 5000 | -2000 | |
| Акции компании B | 1500 | 500 | |
| Вероятность события | 0,6 | 0,4 | |
Эта задача может быть также представлена в виде дерева решений, показанного на рис. 1. На этом рисунке используется два типа вершин: квадратик представляет "решающую" вершину, а кружок — "случайную". Таким образом, из вершины 1 ("решающая") выходят две ветви, представляющие альтернативы, связанные с покупкой акций компании А или В. Далее две ветви, выходящие из "случайных" вершин 2 и 3, соответствуют случаям повышения и понижения котировок на бирже с вероятностями их появления и соответствующими платежами.
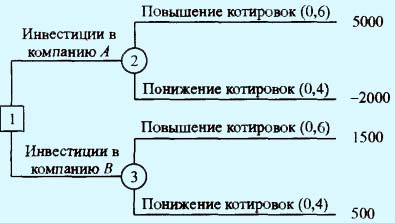
Рис. 1. Дерево решений для задачи инвестирования
Исходя из схемы рис. 1 получаем ожидаемую прибыль за год для каждой из двух альтернатив.
Для акций компании А: 5000 х 0,6 + (-2000) х 0,4 = 2200 (долл.).
Для акций компании В: 1500 х 0,6 + 500 х 0,4 = 1100 (долл.).
Вашим решением, основанным на этих вычислениях, является покупка акций компании А.
На следующем шаге мы приведем несколько задач.
