На этом шаге мы рассмотрим оптимальное решение игры двух лиц с нулевой суммой.
Поскольку игры берут свое начало в конфликте интересов, оптимальным решением игры является одна или несколько таких стратегий для каждого из игроков, при этом любое отклонение от данных стратегий не улучшает плату тому или другому игроку. Эти решения могут быть в виде единственной чистой стратегии или нескольких стратегий, которые являются смешанными в соответствии с заданными вероятностями. Рассматриваемые ниже примеры демонстрируют перечисленные ситуации.
Пример. Две компании А и В продают два вида лекарств против гриппа. Компания А рекламирует продукцию на радио (А1), телевидении (А2) и в газетах (А3). Компания В, в дополнение к использованию радио (B1), телевидения (B2) и газет (B3), рассылает также по почте брошюры (B4). В зависимости от умения и интенсивности проведения рекламной кампании, каждая из компаний может привлечь на свою сторону часть клиентов конкурирующей компании. Приведенная ниже матрица характеризует процент клиентов, привлеченных или потерянных компанией A.
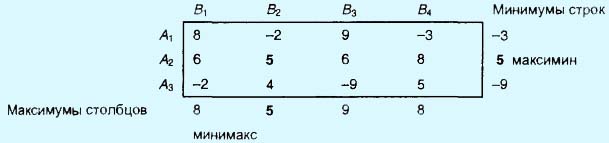
Рис. 1. Матрица характеристик
Решение игры основано на обеспечении наилучшего результата из наихудших для каждого игрока. Если компания A выбирает стратегию A1, то, независимо от того, что предпринимает компания В, наихудшим результатом является потеря компанией А 3% рынка в пользу компании В. Это определяется минимумом элементов первой строки матрицы платежей. Аналогично при выборе стратегии A2 наихудшим исходом для компании А является увеличение рынка на 5% за счет компании В. Наконец, наихудшим исходом при выборе стратегии A3 является потеря компанией А 9% рынка в пользу компании В. Эти результаты содержатся в столбце "Минимумы строк". Чтобы достичь наилучшего результата из наихудших, компания А выбирает стратегию A2, так как она соответствует наибольшему элементу столбца "Минимумы строк".
Рассмотрим теперь стратегии компании В. Так как элементы матрицы являются платежами компании А, критерий наилучшего результата из наихудших для компании В соответствует выбору минимаксного значения. В результате приходим к выводу, что выбором компании В является стратегия B2.
Оптимальным решением в игре является выбор стратегий A2 и B2, т.е. обеим компаниям следует проводить рекламу на телевидении. При этом выигрыш будет в пользу компании А, так как ее рынок увеличится на 5%. В этом случае говорят, что цена игры равна 5% и что компании А и В используют стратегии, соответствующие седловой точке.
Решение, соответствующее седловой точке, гарантирует, что ни одной компании нет смысла пытаться выбрать другую стратегию. Действительно, если компания В переходит к другой стратегии (B1, B3 или B4), то компания А может сохранить свой выбор стратегии A2, что приведет к большей потере рынка компанией B (6 или 8%). По тем же причинам компании А нет резона использовать другую стратегию, ибо если она применит, например, стратегию A3, то компания В может использовать свою стратегию B3 и увеличить свой рынок на 9%. Аналогичные выводы имеют место, если компания А будет использовать стратегию A1.
Оптимальное решение игры, соответствующее седловой точке, не обязательно должно характеризоваться чистыми стратегиями. Вместо этого оптимальное решение может требовать смешивания случайным образом двух или более стратегий, как это сделано в следующем примере.
Пример. Два игрока A и В играют в игру, основанную на подбрасывании монеты. Игроки одновременно и независимо друг от друга выбирают герб (Г) или решку (Р). Если результаты двух подбрасываний монеты совпадают (т.е. ГГ или РР), то игрок А получает один доллар от игрока. Иначе игрок А платит один доллар игроку В.
Следующая матрица платежей игроку А показывает величины минимальных элементов строк и максимальных элементов столбцов, соответствующих стратегиям обоих игроков.

Рис. 1. Матрица платежей
Максиминная и минимаксная величины (цены) для этой игры равны -1 долл. и 1 долл. соответственно. Так как эти величины не равны между собой, игра не имеет решения в чистых стратегиях. В частности, если игрок А использует стратегию AГ, игрок В выберет стратегию BР, чтобы получить от игрока А один доллар. Если это случится, игрок А может перейти к стратегии AР, чтобы изменить исход игры и получить один доллар от игрока В. Постоянное искушение каждого игрока перейти к другой стратегии указывает на то, что решение в виде чистой стратегии неприемлемо. Вместо этого оба игрока должны использовать надлежащую случайную комбинацию своих стратегий. В рассматриваемом примере оптимальное значение цены игры находится где-то между максиминнои и минимаксной ценами для этой игры:
максиминная (нижняя) цена ≤ цена игры ≤ минимаксная (верхняя) цена.
Следовательно, в данном случае цена игры должна лежать в интервале [-1,1], измеряемом в долларах.
На следующем шаге мы приведем несколько задач.
