Шаг 71.
Решение матричных игр в смешанных стратегиях

    На этом шаге мы рассмотрим решение матричных игр в смешанных стратегиях.

    Решение матричных игр в смешанных стратегиях может быть найдено либо графически, либо методами линейного программирования. Графический метод применим для решения игр, в которых хоть один игрок имеет две чистые стратегии. Этот метод интересен в том плане, что графически объясняет понятие седловой точки. Методами линейного программирования может быть решена любая игра двух лиц с нулевой суммой.

    Графическое решение игр. Рассмотрим игру 2 х n, в которой игрок А имеет две стратегии.

Таблица 1. Игра 2 х n

.	y1: B1	y2: B2	...	yn: B4
x1: A1	a11	a12	...	a1n
1-x1: A2	a21	a22	...	a2n

    Игра предполагает, что игрок А смешивает стратегии А₁ и А₂ с соответствующими вероятностями x₁ и 1 - x₁, 0 < x₁ < 1. Игрок Б смешивает стратегии B₁, B₂, ..., B_N с вероятностями y₁, y₂, ..., y_n, где y₁ ≥ 0, j = 1, 2, ..., n, и y₁ + y₂ + ... + y_n = 1. В этом случае ожидаемый выигрыш игрока А, соответствующий j-й чистой стратегии игрока В, вычисляется в виде (a_1j - a_2j)x₁ - a_2j, j = 1, 2, ..., n.

    Следовательно, игрок А ищет величину x_i, которая максимизирует минимум ожидаемых выигрышей

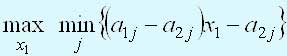
    На следующем шаге мы рассмотрим применение матричных игр в смешанных стратегиях.

Предыдущий шаг Содержание Следующий шаг