На этом шаге мы рассмотрим применение матричных игр в смешанных стратегиях.
Рассмотрим следующую игру 2x4, в которой платежи выплачиваются игроку A.

Игра не имеет решения в чистых стратегиях, и, следовательно, стратегии должны быть смешанными. Ожидаемые выигрыши игрока А, соответствующие чистым стратегиям игрока В, приведены в следующей таблице.
| Чистые стратегии игрока B | Ожидаемые выигрыши игрока А |
|---|---|
| 1 | -2x1 + 4 |
| 2 | -x1 + 3 |
| 3 | x1 + 2 |
| 4 | -7x1 + 6 |
На рис. 1 изображены четыре прямые линии, соответствующие чистым стратегиям игрока В. Чтобы определить наилучший результат из наихудших, построена нижняя огибающая четырех указанных прямых (изображенная на рисунке толстыми линейными сегментами), которая представляет минимальный (наихудший) выигрыш для игрока А независимо от того, что делает игрок В. Максимум (наилучшее) нижней огибающей соответствует максиминному решению в точке x1 = 0,5 . Эта точка определяется пересечением прямых 3 и 4. Следовательно, оптимальным решением для игрока А является смешивание стратегий A1 и A2 с вероятностями 0,5 и 0,5 соответственно. Соответствующая цена игры v определяется подстановкой x1 = 0,5 в уравнение либо прямой 3, либо 4, что приводит к следующему.
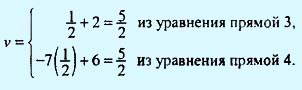
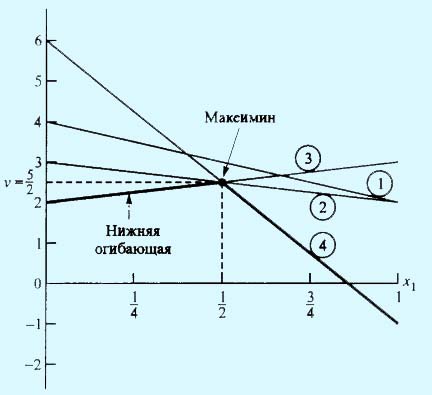
Рис. 1. Графическое решение игры двух лиц с нулевой суммой
Оптимальная смешанная стратегия игрока В определяется двумя стратегиями, которые формируют нижнюю огибающую графика. Это значит, что игрок В может смешивать стратегии B3 и B4, в этом случае y1 = y2 = 0 и y4 = y3. Следовательно, ожидаемые платежи игрока В, соответствующие чистым стратегиям игрока А, имеют такой вид
| Чистые стратегии игрока A | Ожидаемые платежи игрока B |
|---|---|
| 1 | -4y3 - 1 |
| 2 | -4y3 + 6 |
Наилучшее решение из наихудших для игрока В представляет собой точку минимума верхней огибающей заданных двух прямых (построение прямых и определение верхней огибающей будет для вас поучительным). Эта процедура эквивалентна решению уравнения
4y3 - 1 = -4y3 + 6
Его решением будету y3 = 7/8, что определяет цену игры v = 4 х (7/8) - 1 = 5/2.
Таким образом, решением игры для игрока А является смешивание стратегий A1 и A2 с равными вероятностями 0,5 и 0,5, а для игрока В — смешивание стратегий B3 и B4, с вероятностями 7/8 и 1/8. (В действительности игра имеет альтернативное решение для игрока В, так как максиминная точка на рис. 1 определяется более чем двумя прямыми. Любая выпуклая линейная комбинация этих альтернативных решений также является решением задачи.)
Для игры, в которой игрок А имеет m стратегий, а игрок В — только две, решение находится аналогично. Главное отличие состоит в том, что здесь строятся графики функций, представляющих ожидаемые платежи второго игрока, соответствующие чистым стратегиям игрока А. В результате ведется поиск минимаксной точки верхней огибающей построенных прямых.
На следующем шаге мы рассмотрим решение матричных игр методами линейного программирования.
