На этом шаге мы рассмотрим экспоненциальное распределение в системах массового обслуживания.
В большинстве систем массового обслуживания поступление клиентов происходит случайным образом. Это означает, что наступление события (например, поступление клиента или завершение обслуживания) не зависит от времени, прошедшего с момента наступления предыдущего события. Время между последовательными поступлениями клиентов и время их обслуживания, будучи случайными, при моделировании систем массового обслуживания количественно описываются экспоненциальным распределением, плотность вероятности которого имеет вид f(t) = λe-λt, t > 0, где M{t} = 1/λ.
То, что экспоненциальное распределение является совершенно случайным, иллюстрируется следующим примером. Если сейчас 8:20 и некое событие имело место в 8:02, то в соответствии с экспоненциальным законом распределения вероятность того, что следующее аналогичное событие произойдет в 8:29, является функцией лишь интервала времени от 8:20 до 8:29 и не зависит от интервала времени, прошедшего с момента наступления последнего события (от 8:02 до 8:20). Данное свойство экспоненциального распределения обычно называют отсутствием последействия или отсутствием памяти.
Пусть время t наступления какого-либо события распределено по экспоненциальному закону с функцией плотности f(t). Если S - время, прошедшее с момента наступления предыдущего события, то свойство отсутствия последействия выражается соотношением P{t > T + S|t > S} = P{t > T}.
Для доказательства этого равенства заметим, что P{t > Y} = 1 - P{t < Y} = e-λY.
Следовательно, 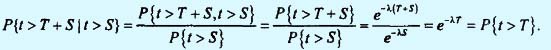
Пример. При обслуживании сложного агрегата всегда существует запасной блок для немедленной замены в случае поломки. Время выхода из строя агрегата (или его запасного блока) является случайной величиной, распределенной по экспоненциальному закону, и в среднем происходит каждые 40 минут. Оператор, обслуживающий агрегат, утверждает, что агрегат "имеет привычку" выходить из строя каждый вечер около 20:30. Проанализируем утверждение оператора.
Средняя интенсивность отказов агрегата равна λ = 60/40 = 1,5 отказа в час. Следовательно, плотность экспоненциального распределения времени отказа имеет вид f(t) = 1,5e-1,5t, t > 0
Что касается заявления оператора, то и без вычислений видно, что оно не может соответствовать действительности, так как не согласуется с тем, что время между отказами агрегата распределено по экспоненциальному закону и, следовательно, является случайным. Для подтверждения или опровержения заявления оператора нельзя использовать вероятность того, что отказ будет происходить в 20:30, так как вероятность такого события зависит от времени дня (относительно 20:30), когда эта вероятность вычисляется. Например, если вычисления выполняются в 20:20, то вероятность того, что утверждение оператора окажется справедливым этим вечером, равна P{t < 10/60} = 1 - e-1,5(10/60) = 0,22, т.е. является очень малой. Если вычисления выполняются в 19:00, то вероятность того, что отказ будет иметь место в 20:30, возрастает примерно до 0,9. Эти два крайних значения вероятности показывают, что достоверность утверждения оператора нельзя проанализировать на основе полученных вероятностей; в данной ситуации мы должны полагаться только на характеристики экспоненциального распределения (точнее, на его свойство отсутствия последействия).
На следующем шаге мы приведем несколько задач.
