На этом шаге мы рассмотрим модель чистого рождения.
Модель обслуживающей системы, представленная только поступлением клиентов называется моделью чистого рождения.
Пусть p0(t) — вероятность отсутствия событий (поступления клиентов) за период времени t. При условии, что длина интервала времени Т между поступлениями клиентов описывается экспоненциальным распределением с интенсивностью λ, будем иметь
p0(t) = P {интервал времени T ≥ t} = 1 - P {интервал времени T ≤ t} = 1 - (1 - e-λt) = e-λt
При достаточно малом интервале времени h > 0 имеем
p0(h) = e-λh = 1 - λh + (λh)2/2! - ... = 1 - λh + O(h2).
Экспоненциальное распределение базируется на предположении, что на достаточно малом временном интервале h > 0 может наступить не более одного события (поступления клиента). Следовательно, при h → 0 p1(h) = 1 - p0(h) ≈ λh.
Этот результат показывает, что вероятность поступления клиента на протяжении интервала h прямо пропорциональна h с коэффициентом пропорциональности, равным интенсивности поступлений λ.
Чтобы получить распределение числа клиентов, поступивших на протяжении некоторого интервала времени, обозначим через pn(t) вероятность поступления n клиентов на протяжении времени t. При достаточно малом h > 0 имеем следующее:
pn(t + h) ≈ pn(t)(1 - λh) + pn-1(t)λh, n > 0,
p0(t + h) ≈ p0(t)(1 - λh), n = 0.
Из первого уравнения следует, что поступление п клиентов на протяжении времени t + h возможно в двух случаях: если имеется n поступлений на протяжении времени t и нет поступлений за время h, или существует n - 1 поступлений за время t и одно поступление за время h. Любые другие комбинации невозможны вследствие того, что на протяжении малого периода h возможно наступление только одного события. В соответствии с условием независимости событий к правой части уравнения применим закон умножения вероятностей. Во втором уравнении отсутствие поступлений клиентов на протяжении интервала t + h возможно лишь тогда, когда нет поступлений клиентов за время h.
Перегруппировывая члены и переходя к пределу при h → 0, получаем следующее.
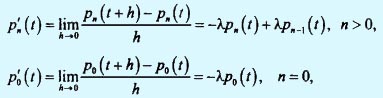
Решение приведенных выше разностно-дифференциальных уравнений имеет следующий вид:
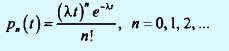
В данном случае мы получили дискретную плотность вероятности распределения Пуассона с математическим ожиданием M{n | t} = λt поступлений за время t. Дисперсия распределения Пуассона также равна λt. Полученный результат означает, что всякий раз, когда временные интервалы между моментами последовательных поступлений заявок распределены по экпоненциальному закону с математическим ожиданием 1/λ, число поступлений заявок в интервале, равном t единиц времени, характеризуется распределением Пуассона с математическим ожиданием λt. Верным является и обратное утверждение. Соответствие между экспоненциальным распределением (с интенсивностью поступлений λ) и распределением Пуассона показано в следующей таблице.
| Экспоненциальное распределение | Распределение Пуассона | |
|---|---|---|
| Слечайная переменная | Время t между наступлениями событий | Количество n наступлений событий в течение заданного периода времени T |
| Значение случайной величины | t ≥ 0 | n = 0, 1, 2, ... |
| Функция плотности вероятности | f(t) = λe-λt, t ≥ 0 | pn(t)=(λt)ne-λt/n!, n = 0, 1, 2, ... |
| Среднее значение (математическое ожидание) | 1/λ временных единиц | λT в течение времени T |
| Функция распределения | P(t ≤ A) = 1 - e-λA | pn ≤ N(T) = p0(T) + p1(T) + ... + pN(T) |
| Вероятность, что не произойдет ни одного события в течение времени A | P(t > A) = e-λA | p0(A) = e-λA |
На следующем шаге рассмотрим применение модели чистого рождения.
