На этом шаге мы рассмотрим применение многоканальной модели обслуживания машинного парка.
Пусть для обслуживания десяти персональных компьютеров (ПК) выделено два инженера одинаковой производительности.
Поток отказов (неисправностей) одного компьютера - пуассоновский с интенсивностью = 2. Время обслуживания ПК
подчиняется показательному закону.
Возможны следующие варианты организации обслуживания:
- оба инженера обслуживают все десять компьютеров, так что при отказе ПК его обслуживает один из свободных инженеров, в этом случае с = 2, N = 10; μ = 8;
- каждый из двух инженеров обслуживает по пять закрепленных за ним ПК. В этом случае с = 1, N = 5.
Необходимо выбрать наилучший вариант организации обслуживания ПК.
С точки зрения теории массового обслуживания инженеры представляют собой обслуживающие устройства, а обслуживание компьютеров является сервисом. Если оба инженера обслуживают все десять компьютеров, то система может быть представлена моделью (М / М / 2) : (GD / 10 / 10) . Если каждый из двух инженеров обслуживает по пять закрепленных за ним ПК, то система может быть представлена моделью (М / М / 1) : (GD / 5 / 5) .
На рис. 1 представлены выходные данные программы TORA для описанной модели (М / М / 2) : (GD / 10 / 10) .
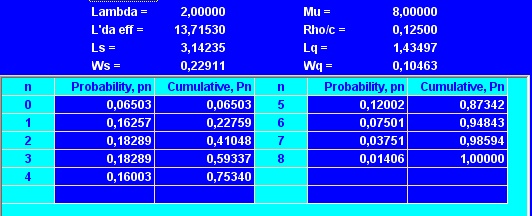
Рис. 1. Результаты расчетов в программе TORA
Исходный файл можно взять здесь.
Получаем следующие результаты:
Cреднее число компьютеров в очереди на обслуживание:
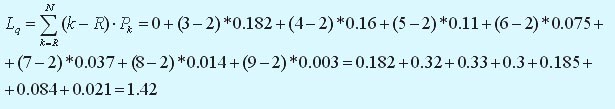
Cреднее число ПК, находящихся в системе (на обслуживании и в очереди):
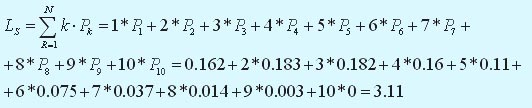
Cреднее число инженеров, простаивающих из-за отсутствия работы:
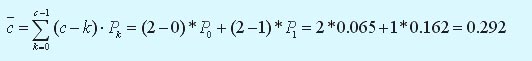
Коэффициент простоя персонального компьютера в очереди следующий:
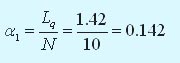
Коэффициент использования компьютеров определяется по формуле:
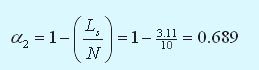
Коэффициент простоя обслуживающих инженеров рассчитывается так:
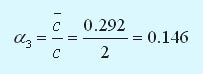
Среднее время ожидания ПК обслуживания
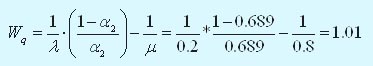
На рис. 2 представлены выходные данные программы TORA для описанной модели (М / М / 1) : (GD / 5 / 5) .
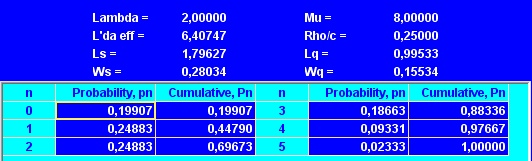
Рис. 2. Результаты расчетов в программе TORA
Исходный файл можно взять здесь.
Получаем следующие результаты:
Cреднее число компьютеров в очереди на обслуживание:
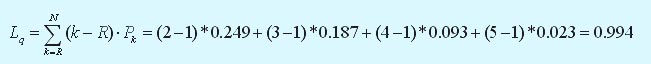
Cреднее число ПК, находящихся в системе (на обслуживании и в очереди):
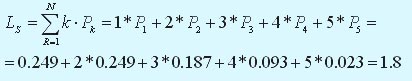
Cреднее число инженеров, простаивающих из-за отсутствия работы:
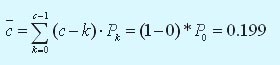
Коэффициент простоя персонального компьютера в очереди следующий:
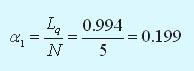
Коэффициент использования компьютеров определяется по формуле:
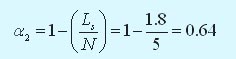
Коэффициент простоя обслуживающих инженеров рассчитывается так:
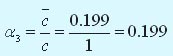
Среднее время ожидания ПК обслуживания
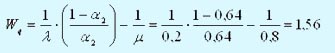
Сведем полученные результаты по двум вариантам в следующую таблицу:
| Итоговые вероятностные характеристики | 1 | 2 |
|---|---|---|
| α1 | 0,142 | 0,199 |
| α2 | 0,689 | 0,64 |
| α3 | 0,146 | 0,199 |
| Wq, час | 1,01 | 1,56 |
Таким образом, в варианте 1 каждый компьютер стоит в очереди в ожидании начала его обслуживания приблизительно 0,142 части рабочего времени, что меньше этого показателя при варианте 2 организации работ. Далее в варианте 1 вероятность того, что ПК и любой момент времени будет работать выше, чем в варианте 2, и равна α21 = 0.689 > α22 = 0.64. Очевидно, вариант 1 организации работ по обслуживанию ПК эффективнее, чем вариант 2.
На следующем шаге рассмотрим введение в динамическое программирование.
