Шаг 109.
Применение задачи о загрузке

    На этом шаге мы рассмотрим применение задачи о загрузке.

    В 4-тонный самолет загружаются предметы трех наименований. Приведенная ниже таблица содержит данные о весе одного предмета w_i (в тоннах) и прибыли r_i (в тысячах долларов), получаемой от одного загруженного предмета. Как необходимо загрузить самолет, чтобы получить максимальную прибыль?

Таблица 1. Данные о весе и прибыли

Предмет i	wi (вес)	ri (прибыль)
1	2	31
2	3	47
3	1	14

    Так как вес одного предмета w_i для всех наименований и максимальный вес W принимают целочисленные значения, состояние x_i может принимать лишь целочисленные значения.

Этап 3. Точный вес, который может быть загружен на этапе 3 (предмет наименования 3), заранее неизвестен, но он должен принимать одно из значений 0, 1, ..., 4 (так как W = 4 тонны). Состояния x₃ = 0 x₃ = 4 представляют собой крайние случаи, когда предметы третьего наименования совсем не загружаются или загружают самолет полностью. Остальные значения x₃ (= 1, 2 или 3) предполагают частичную загрузку самолета предметами третьего наименования. Действительно при этих значениях x₃ все оставшиеся емкости самолета могут быть заполнены предметами третьего наименования.

    Так как вес w₃ одного предмета третьего типа равен 1 тонне, максимальное количество единиц этого типа, которое может быть загружено, равно [4/1] = 4. Это означает, что возможными значениями x₃ будут 0, 1, 2, 3 и 4. Решение m₃ является допустимым лишь при условии, что w₃m₃ < x₃. Следовательно, все недопустимые альтернативы (те, для которых w₃m₃ > x₃) исключены. Следующее уравнение является основой для сравнения альтернатив на этапе 3.

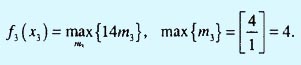
    В следующей таблице сравниваются допустимые решения для каждого значения x₃

Таблица 2. Данные, полученные на этапе 3

x3	m3 = 0	m3 = 1	m3 = 2	m3 = 3	m3 = 4	f3(x3)	m3
0	0	-	-	-	-	0	0
1	0	14	-	-	-	14	1
2	0	14	28	-	-	28	2
3	0	14	28	42	-	42	3
4	0	14	28	42	56	56	4

Этап 2.

Таблица 3. Данные, полученные на этапе 2

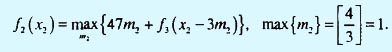
x2	m2 = 0	m2 = 1	f2(x2)	m2
0	0 + 0 = 0	-	0	0
1	0 + 14 = 14	-	14	0
2	0 + 28 = 28	-	28	0
3	0 + 42 = 42	47 + 0 = 47	47	1
4	0 + 56 = 56	47 + 14 = 61	61	1

Этап 1.

Таблица 4. Данные, полученные на этапе 1

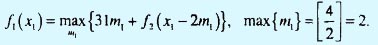
x1	m1 = 0	m1 = 1	m1 = 2	f1(x1)	m1
0	0 + 0 = 0	-	-	0	0
1	0 + 14 = 14	-	-	14	0
2	0 + 28 = 28	31 + 0 = 31	-	31	1
3	0 + 47 = 47	31 + 14 = 45	-	47	0
4	0 + 61 = 61	31 + 28 = 59	62 + 0 = 62	62	2

    Оптимальное решение определяется теперь следующим образом. Из условия W= 4 следует, что первый этап решения задачи при x₁ = 4 дает оптимальное решение m₁ = 2, которое означает, что два предмета первого наименования будут загружены в самолет. Эта загрузка оставляет x₂ = x₁ - 2m₁ = 4 - 2 x 2 = 0. Решение на втором этапе при x₂ = 0 приводит к оптимальному решению 2₂ = 0, которое, в свою очередь, дает x₃ = x₂ - 3m₃ = 0 - 3 x 0 = 0. Далее этап 3 при x₃ = 0 приводит к m₃ = 0.

    Следовательно, оптимальным решением задачи является m₁ = 2, m₂ = 0 и m₃ = 0.

    Соответствующая прибыль равна 62 000 долларов.

    На следующем шаге приведем решение задачи.

Предыдущий шаг Содержание Следующий шаг