Шаг 108.
Задача о загрузке

    На этом шаге мы рассмотрим задачу о загрузке.

    Задача о загрузке - это задача о рациональной загрузке судна (самолета, автомашины и т.п.), которое имеет ограничения по объему или грузоподъемности. Каждый помещенный на судно груз приносит определенную прибыль. Задача состоит в определении загрузки судна такими грузами, которые приносят наибольшую суммарную прибыль.

    Перед тем как представить соотношения динамического программирования, заметим, что рассматриваемая здесь задача известна также как задача о снаряжении, где пилот реактивного самолета должен определить наиболее ценные (необходимые) предметы, которые следует взять на борт самолета, или как задача о рюкзаке, в которой солдат (или турист) должен определить наиболее ценные предметы, подлежащие загрузке в ранец (рюкзак).

    Рекуррентное уравнение процедуры обратной прогонки выводится для общей задачи загрузки судна грузоподъемностью W предметов (грузов) n наименований. Пусть m_i - количество предметов i-го наименования, подлежащих загрузке, w_i - прибыль, которую приносит один загруженный предмет i-го наименования, w_i - вес одного предмета i-го наименования. Общая задача имеет вид следующей целочисленной задачи линейного программирования.

Максимизировать z = r₁m₁ + r₂m₂ + ... + r_nm_n
w₁m₁ + w₂m₂ + ... + w_nm_n = W,
m₁, m₂, ..., m_n > 0 и целые.

    Три элемента модели динамического программирования определяется следующим образом.

1. Этап i ставится в соответствие предмету i-го наименования, i = 1,2,..., n.
2. Варианты решения на этапе i описываются количеством m_i, предметов i-го наименования, подлежащих загрузке. Соответствующая прибыль равна r_im_i. Значение m_i заключено в пределах от 0 до [W/w_i], где [W/w_i] — целая часть числа W/w_i.
3. Состояние x_i, на этапе i выражает суммарный вес предметов, решения о погрузке которых приняты на этапах i, i + 1,..., n. Это определение отражает тот факт, что ограничение по весу является единственным, которое связывает n этапов вместе.

    Пусть f_i(x_i) - максимальная суммарная прибыль от этапов i, i + 1,..., n при заданном состоянии x_i. Проще всего рекуррентное уравнение определяется с помощью следующей двухшаговой

Шаг 1. Выразим f_i(x_i) как функцию f_i+1(x_i+1) в виде

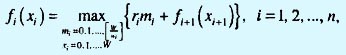
Шаг 2. Выразим x_i+1 как функцию x_i для гарантии того, что левая часть последнего уравнения является функцией лишь x_i. По определению x_i - x_i+1 представляет собой вес, загруженный на этапе i, т.е. x_i - x_i+1 = w_im_i или x_i-1 = x_i - w_im_i. Следовательно, рекуррентное уравнение приобретает следующий вид.

   

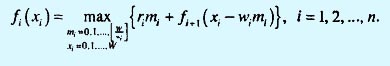
    На следующем шаге рассмотрим применение задачи о загрузке.

Предыдущий шаг Содержание Следующий шаг