Шаг 111.
Задача планирования рабочей силы

    На этом шаге мы рассмотрим задачу планирования рабочей силы.

    При выполнении некоторых проектов число рабочих, необходимых для реализации какого-либо проекта, регулируется путем их найма и увольнения. Поскольку как наем, так и увольнение рабочих связано с дополнительными затратами, необходимо определить, каким образом должна регулироваться численность рабочих в период реализации проекта.

    Предположим, что проект будет выполняться в течение n недель и минимальная потребность в рабочей силе на протяжении i-й недели составит b_i, рабочих. При идеальных условиях хотелось бы на протяжении i-й недели иметь ровно b_i, рабочих. Однако в зависимости от стоимостных показателей может быть более выгодным отклонение численности рабочей силы как в одну, так и в другую сторону от минимальных потребностей.

    Если x_i - количество работающих на протяжении i-й недели, то возможны затраты двух видов:

1. С₁(x_i - b_i) - затраты, связанные с необходимостью содержать избыток x_i - b_i рабочей силы
2. С₂(x_i - x_i-1) - затраты, связанные с необходимостью дополнительного найма x_i - x_i-1 рабочих.

    Элементы модели динамического программирования определяются следующим образом. 3.

1. Этап i представляется порядковым номером недели i, i= 1, 2,..., n.
2. Вариантами решения на i-м этапе являются значения x_i - количество работающих на протяжении i-й недели.
3. Состоянием на i-м этапе является x_i-1 - количество работающих на протяжении (i - 1)-й недели (этапа).

    Рекуррентное уравнение динамического программирования представляется в виде

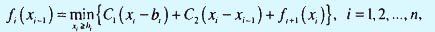
    где f_n+1(x_n) ≡ 0. Вычисления начинаются с этапа n при x_n = b_n и заканчиваются на этапе 1.

    На следующем шаге рассмотрим применение задачи планирования рабочей силы.

Предыдущий шаг Содержание Следующий шаг