На этом шаге мы рассмотрим задачу замены оборудования.
Чем дольше механизм эксплуатируется, тем выше затраты на его обслуживание и ниже его производительность. Когда срок эксплуатации механизма достигает определенного уровня, может оказаться более выгодной его замена. Задача замены оборудования, таким образом, сводится к определению оптимального срока эксплуатации механизма.
Предположим, что мы занимаемся заменой механизмов на протяжении n лет. В начале каждого года принимается решение либо об эксплуатации механизма еще один год, либо о замене его новым. Обозначим через r(t) и c(t) прибыль от эксплуатации t-летнего механизма на протяжении года и затраты на его обслуживание за этот же период. Далее пусть s(t) - стоимость продажи механизма, который эксплуатировался t лет. Стоимость приобретения нового механизма остается неизменной на протяжении всех лет и равна I.
Элементы модели динамического программирования таковы.
- Этап i представляется порядковым номером года i, i = 1, 2, ..., n.
- Вариантами решения на i-м этапе (т.е. для i-го года) являются альтернативы: продолжить эксплуатацию или заменить механизм в начале i-го года.
- Состоянием на i-м этапе является срок эксплуатации t (возраст) механизма к началу i-го года.
Пусть fi(t) - максимальная прибыль, получаемая за годы от i до n при условии, что в начале i-го года имеется механизм t-летнего возраста.
Рекуррентное уравнение имеет следующий вид.
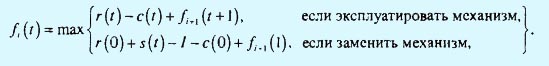
На следующем шаге рассмотрим применение задачи замены оборудования.
