На этом шаге мы рассмотрим применение задачи замены оборудования.
Компания планирует определить оптимальную политику замены используемого в настоящее время трехлетнего механизма на протяжении следующих 4 лет (n = 4), т.е. вплоть до начала пятого года. Таблица 1 содержит относящиеся к задаче данные. Компания требует обязательной замены механизма, который находится в эксплуатации 6 лет. Стоимость нового механизма равна 100 000 долл.
| Возраст t (года) | Прибыль r(t) (долл.) | Стоимость обслуживания c(t) (долл.) | Остаточная стоимость s(t) (долл.) |
|---|---|---|---|
| 0 | 20000 | 200 | - |
| 1 | 19000 | 600 | 80000 |
| 2 | 18500 | 1200 | 60000 |
| 3 | 17200 | 1500 | 50000 |
| 4 | 15500 | 1700 | 30000 |
| 5 | 14000 | 1800 | 10000 |
| 6 | 12200 | 2200 | 5000 |
Определение допустимых значений возраста механизма на каждом этапе является нетривиальной задачей. На рис. 1 представлена рассматриваемая задача замены оборудования в виде сети. В начале первого года имеется механизм, эксплуатирующийся 3 года (на графике рис. 1 по оси Y откладывается возраст механизма). Мы можем либо заменить его (З), либо эксплуатировать (С) на протяжении следующего года. Если механизм заменили, то в начале второго года его возраст будет равен одному году, в противном случае его возраст будет 4 года. Такой же подход используется в начале каждого года, начиная со второго по четвертый.
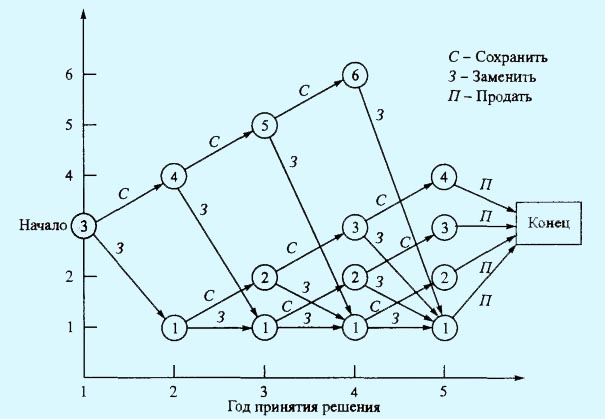
Рис. 1. Схема возможной замены механизма
Если однолетний механизм заменяется в начале второго или третьего года, то заменивший его механизм к началу следующего года также будет однолетним. К тому же, в начале 4-го года 6-летний механизм обязательно должен быть заменен, если он еще эксплуатируется; в конце 4-го года все механизмы продаются (П) в обязательном порядке. На схеме сети также видно, что в начале второго года возможны только механизмы со сроком эксплуатации 1 или 4 года. В начале третьего года механизм может иметь возраст 1, 2 или 5 лет, а в начале четвертого — 1, 2, 3 или 6 лет.
Решение данной задачи эквивалентно поиску маршрута максимальной длины (т.е. приносящего максимальную прибыль) от начала первого года к концу четвертого в сети, показанной на рис. 1. При решении этой задачи используем табличную форму записи. (Числовые данные в таблице кратны тысячам долларов.)
Этап 4.
| . | C | З | Оптимум | |
|---|---|---|---|---|
| t | r(t) + s(t + 1) - c(t) | r(0) + s(t) + s(1) - c(0) - I | f4(t) | Решение |
| 1 | 19,0 + 60 - 0,6 = 78,4 | 20 + 80 + 80 - 0,2 - 100 = 79,8 | 79,8 | З |
| 2 | 18,5 + 50 - 1,2 = 67,3 | 20 + 60 + 80 - 0,2 - 100 = 59,8 | 67,3 | С |
| 3 | 17,2 + 30 - 1,5 = 45,7 | 20 + 50 + 80 - 0,2 - 100 = 4,8 | 49,8 | З |
| 4 | Необходима замена | 20 + 5 + 80 - 0,2 - 100 = 4,8 | 4,8 | З |
Этап 3.
| . | C | З | Оптимум | |
|---|---|---|---|---|
| t | r(t) - c(t) + f4(t + 1) | r(0) + s(t) - c(0) - I + f4(1) | f3(t) | Решение |
| 1 | 19,0 - 0,6 + 67,3 = 85,7 | 20 + 80 - 0,2 - 100 + 79,8 = 79,6 | 85,7 | С |
| 2 | 18,5 - 1,2 + 49,8 = 67,1 | 20 + 60 - 0,2 - 100 + 79,8 = 59,6 | 67,1 | С |
| 5 | 14,0 - 1,8 + 4,8 = 17,0 | 20 + 10 - 0,2 - 100 + 79,8 = 9,6 | 17,0 | З |
Этап 2.
| . | C | З | Оптимум | |
|---|---|---|---|---|
| t | r(t) - c(t) + f3(t + 1) | r(0) + s(t) - c(0) - I + f3(1) | f2(t) | Решение |
| 1 | 19,0 - 0,6 + 67,1 = 85,5 | 20 + 80 - 0,2 - 100 + 85,7 = 85,5 | 85,5 | С или З |
| 4 | 15,5 - 1,7 + 19,6 = 33,4 | 20 + 30 - 0,2 - 100 + 85,7 = 35,5 | 35,5 | З |
Этап 1.
| . | C | З | Оптимум | |
|---|---|---|---|---|
| t | r(t) - c(t) + f2(t + 1) | r(0) + s(t) - c(0) - I + f2(1) | f1(t) | Решение |
| 1 | 17,2 - 1,5 + 35,5 = 51,2 | 20 + 50 - 0,2 - 100 + 85,5 = 55,3 | 55,3 | З |
На рис. 2 показана последовательность получения оптимального решения. В начале первого года оптимальным решением при t = 1 является замена механизма. Следовательно, новый механизм к началу второго года будет находиться в эксплуатации 1 год. При t = 1 в начале второго года оптимальным решением будет либо использование, либо замена механизма. Если он заменяется, то новый к началу третьего года будет находиться в эксплуатации 1 год, иначе механизм будет иметь возраст 2 года. Описанный процесс продолжается до тех пор, пока не будет определено оптимальное решение для четвертого года.
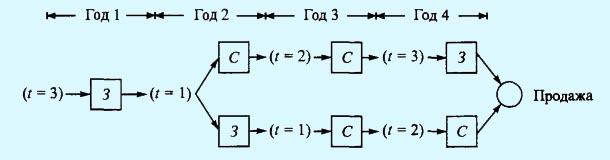
Рис.2. Решение примера
Следовательно, начиная с первого года эксплуатации механизма, альтернативными оптимальными стратегиями относительно замены механизма будут (З, С, С, 3) и (З, 3, С, С). Общая прибыль составит 55 300 долл.
На следующем шаге мы рассмотрим решение задачи.
