На этом шаге мы рассмотрим математический аспект исследования операций.
Типичную математическую модель ИО можно представить следующим высказыванием: Максимизация или минимизация целевой функции при условии выполнения ограничений.
Пример. Среди всех прямоугольников с периметром фиксированной длины L необходимо найти прямоугольник максимальной площади. Какую длину и ширину будет иметь такой прямоугольник?
В этой задаче переменными будут длина l и ширина w прямоугольника. Площадь прямоугольника А вычисляется по формуле А = lw. Таким образом, надо максимизировать величину А при условии, что длина периметра прямоугольника, вычисляемая по формуле 2(1 + w), равна заданной величине L. Математическая модель будет записана следующим образом:
Максимизировать А = lw при ограничении
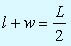 (1)
(1)Эту задачу можно решить, выразив из равенства (1) одну переменную (например, l) через другую (w) и подставив ее в формулу целевой функции. В результате получим следующее.
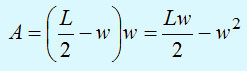
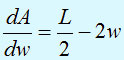
Математический аспект исследования операций обязательно должен рассматриваться в широком контексте всего процесса принятия решений. Это было осознано британскими учеными, которые стали "пионерами" в области ИО еще во время Второй мировой войны. Хотя их работы, в основном, были сосредоточены на оптимизации размещения ограниченных военных ресурсов, в команду разработчиков ИО входили также специалисты по социологии, психологии и поведенческим наукам, что подчеркивало важность человеческого фактора в процессе принятия решений.
В моделях исследования операций переменные, от которых зависят ограничения и целевая функция, могут быть дискретными (чаще всего целочисленными) и континуальными (непрерывными). В свою очередь, ограничения и целевая функция делятся на линейные и нелинейные.
Задачи оптимизации, представленные этими моделями, послужили основой для разработки различных методов решения, которые должны учитывать соответствующие математические свойства этих моделей. Наиболее известными и эффективными из них являются методы линейного программирования, когда целевая функция и все ограничения будут линейными. Для решения математических моделей других типов предназначены методы динамического программирования, целочисленного программирования, нелинейного программирования, многокритериальной оптимизации и методы сетевых моделей.
Практически все методы исследования операций порождают вычислительные алгоритмы, которые являются итерационными по своей природе. Это подразумевает, что задача решается последовательно (итерационно), когда на каждом шаге (итерации) получаем решения, постепенно сходящиеся к оптимальному решению. Итерационная природа алгоритмов обычно приводит к объемным однотипным вычислениям. В этом и заключается причина того, что эти алгоритмы разрабатываются, в основном, для реализации с помощью вычислительной техники.
Использование компьютера как неотъемлемого средства решения задач ИО порождает определенные вычислительные сложности, а именно ошибки машинного округления. Такие ошибки особенно заметны при увеличении числа итераций. Проблема ошибок округления усугубляется, если переменные модели ИО должны принимать только целочисленные значения. Поскольку компьютер все вычисления выполняет в арифметике с плавающей запятой, точное представление некоторых целочисленных значений становится невозможным; в таком случае о решении можно только сказать, что оно принадлежит определенной области значений.
Некоторые математические модели могут быть такими сложными, что их невозможно решить никакими доступными методами оптимизации. В этом случае остается только эвристический подход: поиск подходящего "хорошего" решения вместо оптимального.
Эвристический подход предполагает наличие эмпирических правил, в соответствии с которыми ведется поиск подходящего решения. Обычно эвристические алгоритмы выполняются значительно быстрее, чем алгоритмы нахождения точного решения.
Несмотря на впечатляющие достижения математического моделирования, многие реальные ситуации невозможно адекватно представить с помощью соответствующих математических моделей. В одних случаях в этом "виновата" определенная "жесткость" математики как языка описания и представления событий и явлений. Кроме того, даже если есть возможность формализовать рассматриваемую жизненную ситуацию посредством построения математической модели, полученная на ее основе задача оптимизации может быть слишком сложной для современных алгоритмов решения задач этого класса.
Альтернативой математическому моделированию сложных систем может служить имитационное моделирование. Этот вид моделирования часто является наилучшим (если не единственным) способом исследования реальных систем. Различие между математической и имитационной моделями заключается в том, что в последней отношение между "входом" и "выходом" модели может быть явно не задано.
Вместо явного математического описания взаимоотношения между входными и выходными переменными математической модели, при имитационном моделировании реальная система разбивается на ряд достаточно малых (в функциональном отношении) элементов или модулей. Затем поведение исходной системы имитируется как поведение совокупности этих элементов, определенным образом связанных (путем установления соответствующих взаимосвязей между ними) в единое целое. Вычислительная реализация такой модели начинается с входного элемента, далее проходит по всем элементам, пока не будет достигнут выходной элемент модели.
Вычислительные аспекты имитационных моделей обычно сравнительно несложные, но, как правило, очень трудоемкие. Поэтому реализация таких моделей подразумевает использование вычислительной техники.
Имитационные модели значительно гибче в представлении реальных систем, чем их математические "конкуренты". Причина такой гибкости заключается в том, что при имитационном моделировании исходная система рассматривается на элементном уровне, в то время как математические модели стремятся описать системы на глобальном, как можно более общем уровне.
Но за гибкость имитационных моделей приходится платить высокими требованиями к потребляемым временным и вычислительным ресурсам. Поэтому реализация некоторых имитационных моделей даже на современных быстрых и высокопроизводительных компьютерах может быть очень медленной.
Решения реальных задач исследования операций должны быть плодом коллективной работы, когда бок о бок работают аналитики ИО и клиент-заказчик задачи принятия решений. Аналитикам ИО с их знаниями возможностей математического моделирования необходимы опыт и знание реальной ситуации, исходящие от клиента, для которого, собственно, и решается задача ИО.
Исследование операций, как инструмент задачи принятия решения, можно рассматривать и как науку, и как искусство. Наука здесь представлена всей мощью математических методов, а искусство — тем обстоятельством, что успех на всех этапах, предшествующих получению оптимального решения математической модели, в большей степени зависит от творчества и опыта всей команды, занимающейся решением задачи ИО.
На следующем шаге рассмотрим этапы реализации методов исследования операций.
