На этом шаге мы рассмотрим пример задачи линейного программирования.
Компания "Русские краски" производит краску для внутренних и наружных работ из сырья двух типов: Ml и М2. Следующая таблица представляет основные данные для задачи.
| Расход сырья на тонну краски | Максимально возможный ежедневный расход сырья |
||
|---|---|---|---|
| Для наружных работ | Для внутренних работ | ||
| Сырье М1 | 6 | 4 | 24 |
| Сырье М2 | 1 | 2 | 6 |
| Доход, руб. на тонну |
5 | 4 | - |
Отдел маркетинга компании ограничил ежедневное производство краски для внутренних работ до 2 т (из-за отсутствия надлежащего спроса), а также поставил условие, чтобы ежедневное производство краски для внутренних работ не превышало более чем на тонну аналогичный показатель производства краски для внешних работ. Компания хочет определить оптимальное (наилучшее) соотношение между видами выпускаемой продукции для максимизации общего ежедневного дохода.
Задача (модель) линейного программирования, как и любая задача исследования операций, включает три основных элемента.
- Переменные, которые следует определить.
- Целевая функция, подлежащая оптимизации.
- Ограничения, которым должны удовлетворять переменные.
Определение переменных — первый шаг в создании модели. После определения переменных построение ограничений и целевой функции обычно не вызывает трудностей.
В нашем примере необходимо определить ежедневные объемы производства краски для внутренних и наружных работ. Обозначим эти объемы как переменные модели: x1 — ежедневный объем производства краски для наружных работ; х2 — ежедневный объем производства краски для внутренних работ.
Используя эти переменные, далее строим целевую функцию. Логично предположить, что целевая функция, как суммарный ежедневный доход, должна возрастать при увеличении ежедневных объемов производства красок. Обозначим эту функцию через z (она измеряется в тысячах руб) и положим, что Z = 5x1 + 4x2.
В соответствии с целями компании получаем задачу: Максимизировать Z = 5x1 + 4x2.
Итак, остался не определенным последний элемент модели — условия (ограничения), которые должны учитывать ограниченные возможности ежедневного потребления сырья и ограниченность спроса на готовую продукцию. Другими словами, ограничения на сырье можно записать следующим образом.
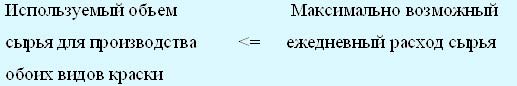
Из таблицы с данными имеем следующее.
Используемый объем сырья Ml = 6x1 + 4х2 (т)
Используемый объем сырья М2 = 1x1 + 2х2 (т)
Так как ежедневный расход сырья Ml и М2 ограничен соответственно 24 и 6 тоннами, получаем следующие ограничения. 6x1 + 4х2 ≤ 24 (сырье Ml) x1 + 2x2 ≤ 6 (сырье М2)
Существует еще два ограничения по спросу на готовую продукцию: (1) максимальный ежедневный объем производства краски для внутренних работ не должен превышать 2 т и (2) ежедневный объем производства краски для внутренних работ не должен превышать ежедневный объем производства краски для наружных работ более чем на одну тонну. Первое ограничение простое и записывается как х2 ≤ 2.
Второе можно сформулировать так: разность между ежедневными объемами производства красок для внутренних и наружных работ не должна превышать одной тонны, т.е. х2 – x1 ≤ 1.
Еще одно неявное ограничение состоит в том, что переменные x1 и х2 должны быть неотрицательными. Таким образом, к сформулированным выше ограничениям необходимо добавить условие неотрицательности переменных.
Окончательно задача будет записана следующим образом:
Максимизировать z = 5х1 + 4х2 при выполнении ограничений
6х1 + 4х2 ≤ 24,
x1 + 2х2 ≤ 6,
-x1 + 2x2 ≤1
х2 ≤ 2,
х1 ≥ 0, х2 ≥ 0.
Любое решение, удовлетворяющее ограничениям модели, является допустимым. Например, решение x1 = 3 и х2 = 1 будет допустимым, так как не нарушает ни одного ограничения, включая условие неотрицательности. Значение целевой функции при этом решении будет равно z = 19 (тысяч руб.).
Итак, задача сформулирована, теперь встает вопрос о нахождении оптимального допустимого решения, доставляющего максимум целевой функции. Можно сделать вывод, что задача имеет много (фактически, бесконечно много) допустимых решений. По этой причине невозможна подстановка значений переменных для поиска оптимума, т.е. нельзя применить простой перебор всех допустимых решений. Следовательно, необходима эффективная процедура отбора допустимых решений для поиска оптимального.
На следующем шаге мы приведем решение этой задачи с помощью программы Tora.
