На этом шаге мы рассмотрим реализацию задачи линейного программирования в программе Tora.
1. Запустите программу Tora.exe. В результате будет отображено окно (рис. 1). Нажмите любую клавишу для входа в программу.
Рис. 1. Окно прграмы TORA
2. Будет отображено окно с меню (рис. 2). Для решения задач линейного программирования выберите (Linear programming).
Рис. 2. Окно меню
3. В результате будет открыто подменю (рис. 3):
Рис. 3. Окно подменю
1) Прочитать созданный файл данных задачи (необходимо ввести полный путь к файлу *.or)
2) Ввести новую задачу
Выберите второй вариант.
4. На экране будет отображено окно с формой для ввода данных задачи (рис. 4):
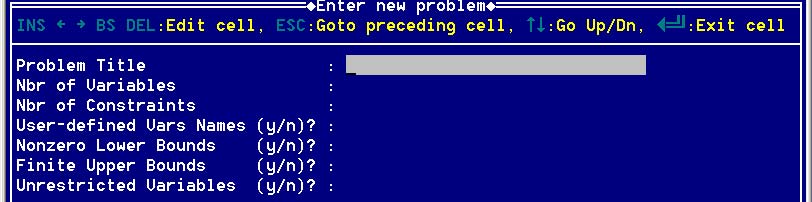
Рис. 4. Окно формы
В верхней строке рабочего окна укажите имя задачи (Problem Title); это произвольный идентификатор (но русские буквы программа не понимает). Вторая строка — число переменных (Nbr of Variables); после выхода из ячейки программа сообщает, что по умолчанию присвоила переменным имена xi, где i — номер переменной. Третья строка — число ограничений (Nbr of constraints). Следующие четыре строки запрашивают, желает ли пользователь дать переменным оригинальные имена (User-Defined Vars Names), задать ненулевые нижние границы (Nonzero Lower Bounds) и верхние границы (Finite Upper Bounds) изменения переменных, ввести неограниченные по знаку переменные (Unrestricted Variables). Во всех случаях по умолчанию принято "нет", поэтому при входе в ячейку в ней появляется буква n; нужно либо ввести y ("да"), либо уйти из ячейки. Если хотя бы в одной из этих строк принятое по умолчанию значение было изменено, то на одном из последующих шагов программа запросит необходимую дополнительную информацию.
В поля формы последовательно введите следующие значения:
1) Имя проблемы - Reddy Mikks
2) Количество переменных – 2 (x1 — ежедневный объем производства краски для наружных работ; х2 — ежедневный объем производства краски для внутренних работ)
3) Количество ограничений – 4 (не учитывать указание неотрицательности переменных)
4) Оригинальные имена – да
5) Задать ненулевые нижние границы - нет
6) Задать верхние границы – нет
7) Ввести неограниченные по знаку переменные – нет
В результате получим следующую форму (рис. 5):
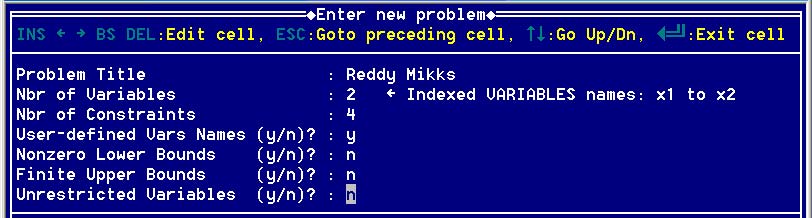
Рис. 5. Окно формы
Нажмите клавишу Enter. Появится строка для ввода имен переменных рис. 6 (под х1 введите – Int (для наружных работ); под х2 введите – Ext (для внутренних работ)). Нажмите Enter.
 →
→ 
Рис. 6. Строка для ввода имен переменных
Появится строка для ввода коэффициентов целевой функции (рис. 7):
 →
→ 
Рис. 7. Строка для ввода коэффициентов функции
Выберите одно из значений (max – максимизировать (по умолчанию), min – минимизировать (для изменения введите m)). Введите в поле (под х1) значение 5. Нажмите Enter. В поле под х2 введите 4. Нажмите Enter.
На следующих шагах нужно внести ограничения (Constraint 1 - 4) рис. 8. Введем первое ограничение:
1) х1 – 6
2) х2 – 4
3) символ ≤ оставим без изменения (для изменения символа нужно ввести нужный с клавиатуры)
4) свободный член (RHS) – 24
 →
→ 
Рис. 8. Ввод ограничений
Аналогично введите остальные три ограничения. После ввода Constraint 4 нажмите F8. Последует сообщение о сохранении файла данных (нажмите y) и введите путь и имя файла с расширением or. (рис. 9).

Рис. 9. Сохранение файла данных
Нажмите Enter.
5. В результате будет отображено меню решения/ модификации задачи (рис. 10).
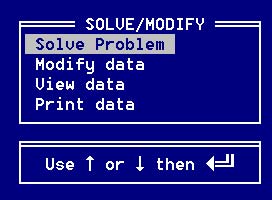
Рис. 10. Окно меню решения и модификации задачи
1) Solve Problem – решить задачу
2) Modify data – изменить данные задачи
3) View data – просмотреть данные задачи
4) Print data – вывести на печать (или в файл)
Выберите - решить задачу. В результате будет открыто подменю предлагающее произвести решение автоматически (Automated procedure) или под управлением пользователя (User-guided procedure). В этом меню стоит выбрать автоматическое решение.
Рис. 11. Окно подменю
Затем в появившемся меню выбрать (View solution / sensitivity summery) – просмотреть результат и провести анализ чувствительности.
Рис. 12. Окно выбора действий
6. В результате проделанных действий должен получиться следующий результат (рис. 13):
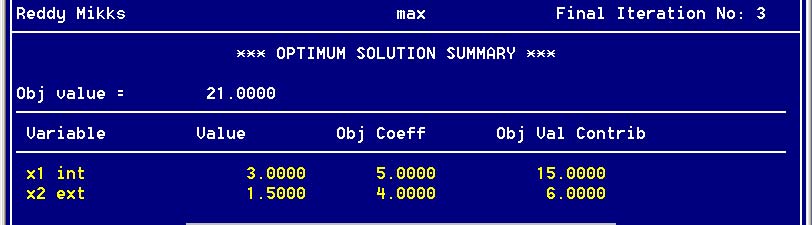
Рис. 13. Результат решения задачи
1) В верхней строке указано имя проблемы, задача (максимизация) и количество итераций (3)
2) Следует раздел Optimum solution summary – итоговая сводка оптимального решения, который предоставляет следующую информацию:
а. Obj value – значение целевой функции при найденном оптимальном решении (доход - 21.0000)
б. Variable – имена переменных
в. Value – оптимальные значения переменных
г. Obj Coeff – коэффициент целевой функции
д. Obj Val Contrib – произведение оптимального значения на значение коэффициента целевой функции
Далее следует сообщение о том, что для перехода к новому разделу (или для продолжения просмотра текущего) следует нажать кнопку PgDn, а для возврата к предыдущему – PgUp. Перейдите к следующей таблице раздела Optimum solution summery, в которой предоставлена информация об ограничениях (Constraint) рис. 14.
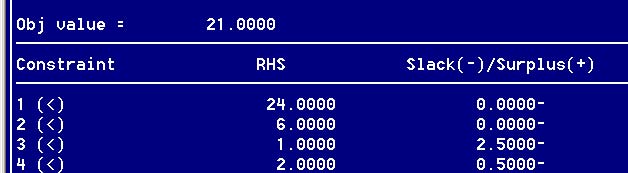
Рис. 14. Информация об ограничениях
В столбце Slack(-)/Surplus(+) указаны значения дополнительных переменных (остаточных (-) и избыточных (+)). В задаче все дополнительные переменные являются остаточными. Значения дополнительных переменных для первых двух неравенств равны нулю, следовательно, сырье М1 и М2 будут использованы полностью, в третьем и четвертом ограничении остаточные переменные отличны от нуля, следовательно, неравенства этих ограничений выполняются строго. Для перехода к новому разделу нажмите PgDn.
7. В результате будет открыт раздел Sensitivity analysis (анализ чувствительности). В таблице приводится результаты анализа чувствительности при изменении по отдельности (single changes) коэффициентов целевой функции (таблица Obj Coeffs). Например, текущее оптимальное решение сохраняется до тех пор, пока доход на тонну краски для внешних работ составляет от 2 тыс. до 6 тыс.
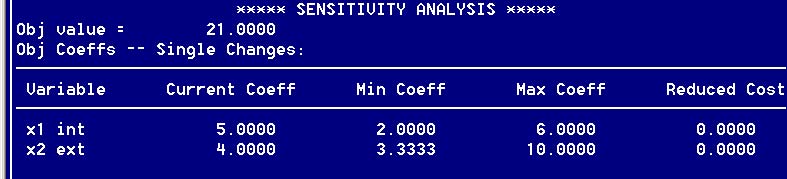
Рис. 15. Раздел анализа чувствительности
Столбец Reduced Cost (Приведенная цена). С точки зрения экономиста переменные в модели ЛП можно рассматривать как числовые характеристики интенсивности определенных видов деятельности (или процессов), в результате которых потребляются ресурсы ("вход" модели) в целях получения прибыли ("выход" модели). Из этой интерпретации вытекает следующее определение.

Если приведенная стоимость какого-либо процесса положительна, то отсюда следует, что стоимость потребленных ресурсов больше возможного дохода (все на единицу интенсивности процесса), поэтому такой процесс экономически не приемлем. Это обуславливает нулевое значение соответствующей переменной в оптимальном решении. Если же экономически привлекательный процесс имеет нулевую приведенную стоимость, то это означает, что достигнута точка равновесия, когда "выход" (единичный доход) равен "входу" (единичной стоимости ресурсов). В оптимальном решении обе переменные х1 и х2 имеют положительные значения и нулевые приведенные стоимости. Для перехода к новой таблице данного раздела нажмите PgDn.
8. На новой странице представлены данные таблицы значений правых частей неравенств ограничений (Righthand side) рис. 16.
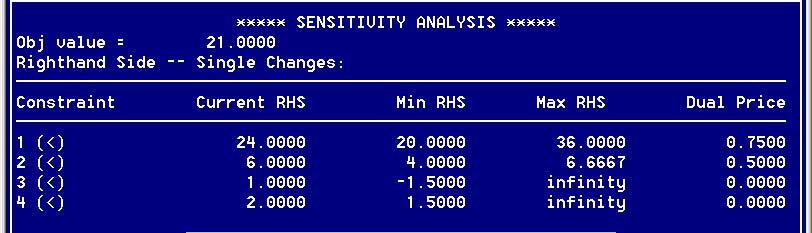
Рис. 16. Таблица значений
Например, текущее оптимальное решение будет сохранено, если ежедневные поступления сырья М1 (ограничение 1) будет находиться в пределах от 20 до 36 тонн. В столбце Dual Price (Двойственная цена) указана стоимость единицы материала. Теперь рассмотрим определение двойственной цены. Двойственная цена — это просто еще одно название стоимости единицы ресурсов. Она равна вкладу, который привносит в значение целевой функции изменение на одну единицу лимита, определяющего доступность ресурса. Термин "двойственная цена" произошел от названия "проблема двойственности" из теории линейного программирования. Хотя название "стоимость единицы ресурсов" лучше отображает смысл, вкладываемый в это понятие, мы все же будем использовать термин "двойственная цена" (dual price), так как он применяется во всех коммерческих программах решения задач ЛП.
Двойственные цены для сырья M1 и М2 равны соответственно 0.75 и 0.5 (т.е. $750 и $500) за тонну (здесь через M1 и М2 обозначено количество материалов М1 и М2 соответственно). Отсюда следует, что если, например, доступное количество сырья Ml возрастет от текущего уровня в 24 т до 28, тогда оптимальное значение целевой функции увеличится на $750 х (28 - 24) = $3000.
Двойственные цены для третьего и четвертого ограничений в данной модели равны нулю при изменении значений правых частей этих неравенств от 0 до ∞ и от 1.5 до ∞ соответственно. Это означает, что ограничения, накладываемые рынком на структуру производства (ограничение на производство краски для внутренних работ до 2 т и т.п.), в данной ситуации не оказывают влияния на оптимальное решение. Для отображения новой таблицы данного раздела нажмите PgDn.
9. В таблице Objective Coefficients (рис. 17) приведены результаты анализа влияния на оптимальное решение одновременного изменения (Simultaneous changes) всех коэффициентов целевой функции.
Чтобы отследить результат одновременного изменения коэффициентов целевой функции, в данной модели представим эту функцию как z = (5 + d1)x1 + (4 + d2)x2. Тогда условие неотрицательности, накладываемое на дополнительные переменные sx3 и sx4 первого и второго ограничений, будет записано в виде следующих неравенств:
0.05 - 0.50d1 + 0.750d2 ≥ 0
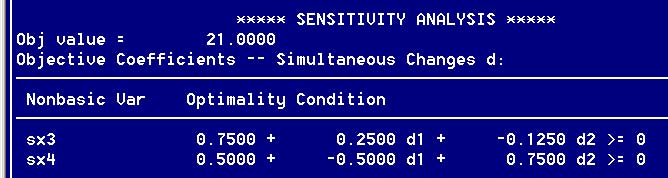
Рис. 17. Результаты анализа при изменении коэффициентов целевой функции
Эти неравенства эквивалентны системе неравенств 1/2 ≤ c1/c2 ≤ 6/4. Для того чтобы убедиться в эквивалентности этих неравенств, подставьте в последние из них выражения с1 = 5+ d1 и с2 = 4 + d2 и выполните необходимые действия (проверьте!).
Отметим, что при вариации d1 и d2 в пределах, не нарушающих приведенных неравенств, изменяется только оптимальное значение целевой функции; значения переменных остаются неизменными. Если измененные значения d1 и d2 не удовлетворяют неравенствам, то необходимо искать новое оптимальное решение. Для продолжения просмотра таблиц данного раздела нажмите PgDn.
10. В результате будет отображена последняя таблица хода решения проблемы Right-hand side ranging (результаты анализа влияния на оптимальное решение одновременного изменения значений правых частей всех неравенств) рис. 18.
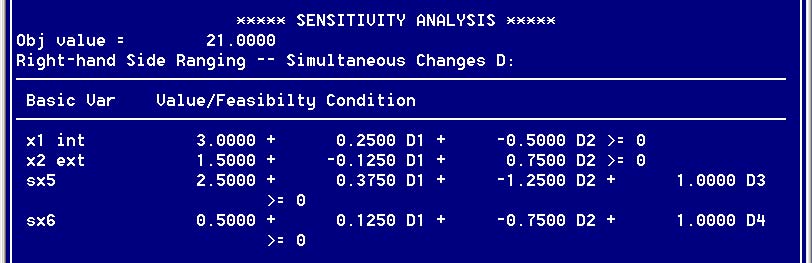
Рис. 18. Результат анализа при изменении значений
правых частей всех неравенств
В данной модели представим правые части неравенств как 24 + D1, 6 + D2, 1 + D3 и 2 + D4. Тогда оптимальные значения переменных можно выразить через новые переменные D1, D2, D3 и D4 (соответствующие формулы показаны в таблице Right-hand Side Ranging — Simultaneous Changes на рис. 18). Для того чтобы решение было осуществимым, необходимо выполнение условия неотрицательности для значений переменных в оптимальном решении — тем самым накладываются ограничения на новые переменные D1, D2, D3 и D4.
Например, положим D1 = 5, D2 = -1, D3 = 1 и D4 = 2. Тогда
x1 = 3 + 0.25 * 5 - 0.5 * (-1) = 4.75
x2 = 1.5 - 0.125 * 5 + 0.75 * (-1) = 0.125
sx5 = 2,5 + 0.375 * 5 – 1,25 * (-1) + 1 * 1 = 6.625
sx6 = 0.5 + 0.125 * 5 - 0.75 * (-1) + 1 * 2 = 3.875
Здесь значения всех переменных положительные. Следовательно, имеем оптимальное решение x1 = 4.75 т, х2 = 0.125 т и z = 5 * 4.75 + 4 * 0.125= 24.25 (т.е. 24 250). Полученное значение z больше текущего оптимального на величину z = 24 250 - 21 000 = 3 250. Эту разность можно подсчитать также по формуле z = D1y1 + D2y2 + D3y3+ D4y4, где у1, у2, у3 и у4 — двойственные цены соответствующих ресурсов. На основании последней формулы получаем z = 5 * 750 + (-1) * 500 + 1 * 0 + 2 * 0 = 3250.
Этот способ вычислений применим только тогда, когда изменения Di, i = 1, 2, 3, 4, приводят к допустимому решению. Если в результате изменений правых частей ограничений значение какой-нибудь переменной будет отрицательным, то это означает, что необходимо искать новую точку оптимального решения.
Файл с задачей можно взять здесь.
На следующем шаге мы рассмотрим решение этой же задачи с помощью Microsoft Excel.
