Шаг 14.
Графическое решение задач линейного программирования

    На этом шаге мы рассмотрим графический метод решения задач линейного программирвоания.

    Графически способ решения задач линейного программирования целесообразно использовать:

1. Для решения задач с двумя переменными, когда ограничения выражены неравенствами;
2. Решения задач со многими переменными при условии, что в их канонической записи содержится не более двух свободных переменных.

    Запишем задачу линейного программирования с двумя переменными:

целевая функция: Z_max = c₁x₁ + c₂x₂        (1)
ограничения: 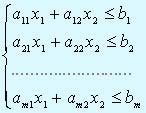        (2)
x₁ ≥ 0, x₂ ≥ 0.        (3)

    Каждое из неравенств (2) – (3) системы ограничений задачи геометрически определяет полуплоскость соответственно с граничными прямыми a_i1x_i1 + a_i2x_i2 = b_i, i=1, 2, ..., m; х₁ = 0; х₂ = 0. В том случае, если система неравенств (2) – (3) совместна, область ее решений есть множество точек, принадлежащих всем указанным полуплоскостям. Так как множество точек пересечения данных полуплоскостей – выпуклое, то областью допустимых значений является выпуклое множество, которое называется многоугольником решений. Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки равенств.

    Поскольку x₁ и x₂ должны быть неотрицательными, то их допустимые значения всегда будут находиться выше оси x₁ и правее оси x₂ , т.е. в I-м квадранте.

    Областью допустимых решений системы неравенств (2) – (3) может быть:

• выпуклый многоугольник;
• выпуклая многоугольная неограниченная область;
• пустая область;
• луч;
• отрезок;
• единственная точка.

    Целевая функция (1) определяет на плоскости семейство параллельных прямых, каждой из которых соответствует определенное значение Z.

    Вектор 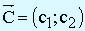с координатами из коэффициентов ЦФ при x₁ и x₂ перпендикулярен к каждой из линий уровня. Направление вектора 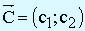совпадает с направлением возрастания ЦФ, что является важным моментом для решения задач. Направление убывания ЦФ противоположно направлению вектора .

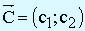    Суть графического метода заключается в следующем. По направлению (против направления) вектора 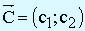в ОДР производится поиск оптимальной точки X^* = (x₁^*;x₂^*). Оптимальной считается точка, через которую проходит линия уровня L_max ( L_min ), соответствующая наибольшему (наименьшему) значению функции L(X). Оптимальное решение всегда находится на границе ОДР, например, в последней вершине многоугольника ОДР, через которую пройдет целевая прямая, или на всей его стороне.

    При поиске оптимального решения задач ЛП возможны следующие ситуации:

• существует единственное решение задачи;
• существует бесконечное множество решений (альтернативный оптимум);
• ЦФ не ограничена;
• область допустимых решений – единственная точка;
• задача не имеет решений.

    Если в одной и той же системе координат изобразить область допустимых решений системы неравенств (2) – (3) и семейство параллельных прямых (1), то задача определения максимума функции Z сведется к нахождению в допустимой области точки, через которую проходит прямая из семейства Z = const, и которая соответствует наибольшему значению параметра Z.

    Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху. При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение.

    Для определения данной вершины построим линию уровня Z = c₁x₁ + c₂x₂ = 0, проходящую через начало координат и перпендикулярную вектору 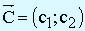, и будем передвигать ее в направлении вектора 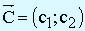до тех пор, пока она не коснется последней крайней (угловой) точки многоугольника решений.

    Координаты указанной точки определяют оптимальный план данной задачи.

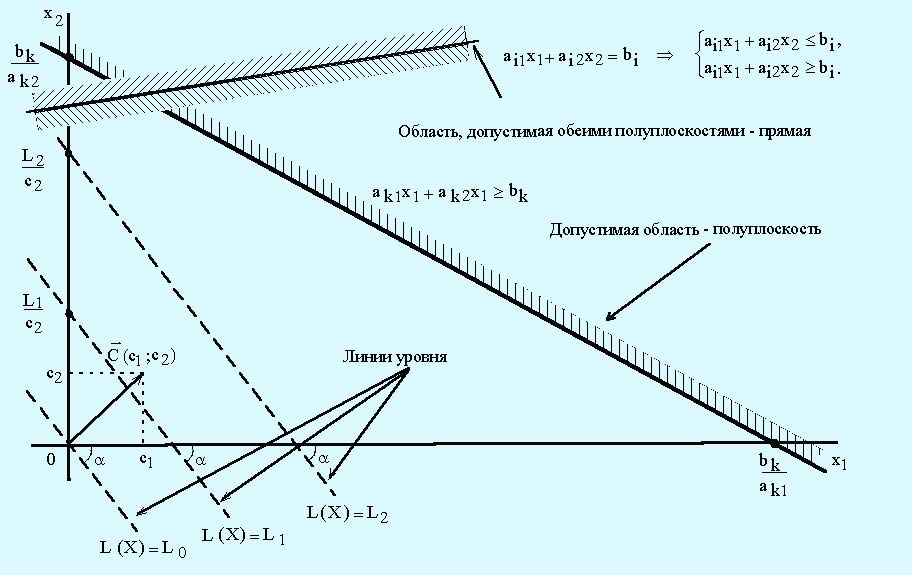
Рис. 1. Графический метод решения задачи линейного программирования

    Отметим, что нахождение минимального значения Z при данной системе ограничений отличается от нахождения ее максимального значения при тех же ограничениях лишь тем, что линия уровня Z передвигается не в направлении вектора 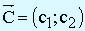, а в противоположном направлении. Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении ее минимального значения.

    Для практического решения задачи линейного программирования (1) – (3) на основе ее геометрической интерпретации необходимо следующее:

1. Построить прямые, уравнения которых получаются в результате замены в ограничениях (2) – (3) знаков неравенств на знаки равенств.
2. Найти полуплоскости, определяемые каждым из ограничений.
3. Определить многоугольник решений.
4. Построить вектор .
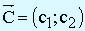5. Построить прямую Z = c₁x₁ + c₂x₂ = 0, проходящую через начало координат и перпендикулярную вектору .
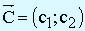6. Передвигать прямую Z в направлении вектора 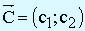, в результате чего либо находят точку (точки), в которой функция принимает максимальное значение, либо устанавливают неограниченность функции сверху на множестве планов.
7. Определить точки координаты максимума функции и вычислить значение целевой функции в этой точке.

    Далее графический способ решения опишем в двух вариантах: для максимизации и минимизации целевой функции.

Предыдущий шаг Содержание Следующий шаг