На этом шаге рассмотрим пример на определение решений системы уравнений.
Рассмотрим систему двух уравнений с пятью неизвестными (m = 2, n = 5).
x1 + x2 + 4x3 + 2x4 + 3x5 = 8,
4x1 + 2x2 + 2x3 + x4 + 6x5 = 4.
Определим различные решения этой системы. Количество положительных базисных решений равно 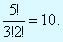 По определению базисное решение включает только две переменные, предполагая, что небазисных нулевых переменных три.
По определению базисное решение включает только две переменные, предполагая, что небазисных нулевых переменных три.
- Допустимое базисное решение.
Нулевые (небазисные) переменные: x2, x4, x5.
Уравнения: x1 + 4x3 = 8, 4x1 + 2x3 = 4.
Решение: единственное решение x1 = 0, x3 = 2.
Заключение: базисное решение допустимо, т.к. x1, x3 ≥ 0.
- Недопустимое базисное решение.
Нулевые (небазисные) переменные: x3, x4, x5.
Уравнения: x1 + x2 = 8, 4x1 + 2x2 = 4.
Решение: единственное решение x1 = -6, x2 = 14.
Заключение: базисное решение недопустимо, т.к. x1 < 0.
- Решение не единственное.
Нулевые (небазисные) переменные: x1, x2, x5.
Уравнения: 4x3 + 2x4 = 8, 2x3 + x4 = 4.
Решение: единственного решения не существует, т.к. уравнения зависимы.
Заключение: бесконечное количество решений.
- Решения не существует.
Нулевые (небазисные) переменные: x1, x3, x4.
Уравнения: x2 + 3x5 = 8, 2x2 + 6x5 = 4.
Решение: решения не существует, т.к. уравнения несовместны.
Заключение: решения не существует.
- Недопустимое базисное решение
Нулевые (небазисные) переменные: x2, x3, x5.
Уравнения: x1 + 2x4 = 8, 4x1 + x4 = 4.
Решение: единственное решение x1 = 14, x4 = -3.
Заключение: базисное решение недопустимо, т.к. x4 < 0.
- Допустимое базисное решение
Нулевые (небазисные) переменные: x2, x3, x4.
Уравнения: x1 + 3x5 = 8, 4x1 + 6x5 = 4.
Решение: единственное решение x1 = 10/3, x5 = 14/9.
Заключение: базисное решение допустимо, т.к. x1, x5 ≥ 0.
- Допустимое базисное решение.
Нулевые (небазисные) переменные: x1, x4, x5.
Уравнения: x2 + 4x3 = 8, 2x2 + 2x3 = 4.
Решение: единственное решение x2 = 0, x3 = 2.
Заключение: базисное решение допустимо, т.к. x2, x3 ≥ 0.
- Допустимое базисное решение.
Нулевые (небазисные) переменные: x1, x3, x5.
Уравнения: x2 + 2x4 = 8, 2x2 + x4 = 4.
Решение: единственное решение x2 = 0, x4 = 4.
Заключение: базисное решение допустимо, т.к. x2, x4 ≥ 0.
- Допустимое базисное решение.
Нулевые (небазисные) переменные: x1, x2, x4.
Уравнения: 4x3 + 3x5 = 8, 2x3 + 6x5 = 4.
Решение: единственное решение x3 = 2, x5 = 0.
Заключение: базисное решение допустимо, т.к. x3, x5 ≥ 0.
- Допустимое базисное решение.
Нулевые (небазисные) переменные: x1, x2, x3.
Уравнения: 2x4 + 3x5 = 8, x4 + 6x5 = 4.
Решение: единственное решение x4 = 4, x5 = 0.
Заключение: базисное решение допустимо, т.к. x4, x5 ≥ 0.
На следующем шаге рассмотрим свободные переменные и базисные решения.
