На этом шаге рассмотрим процесс определения базисных решений задачи линейного программирования.
Задача линейного программирования, записанная в стандартной форме, содержит m линейных равенств с n неизвестными переменными (m < n).
Разделим n переменных на два множества:
- n - m переменные, которые положим равными нулю,
- оставшиеся m переменные, значения которых определяются как решение системы из m линейных уравнений.
Если это решение единственное, тогда соответствующие m переменные называются базисными, а остальные n - m нулевые переменные — небазисными.
В этом случае результирующие значения переменных составляют базисное решение.
Если все переменные принимают неотрицательные значения, то такое базисное решение является допустимым. В противном случае — недопустимым.
Основываясь на этих определениях, нетрудно подсчитать, что количество всех положительных базисных решений для m уравнений с n неизвестными не превосходит 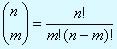 .
.
На следующем шаге рассмотрим пример на определение всех базисных решений некоторой системы уравнений.
