На этом шаге рассмотрим решение задачи линейного программирования двухэтапным методом.
Решим задачу линейного программирования с помощью двухэтапного метода:
Минимизировать 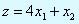 .
.
При условиях: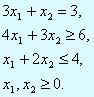
Этап 1.
Минимизировать 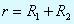
С ограничениями 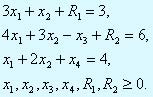
Соответствующая таблица имеет вид:
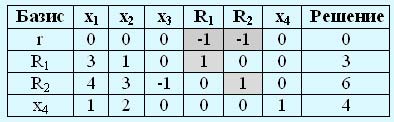
Вычислим новую r-строку

В результате получим следующее оптимальное решение:
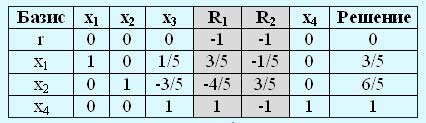
Поскольку достигнут минимум r = 0, значит, на первом этапе получено допустимое базисное решение x1 = 3/5, x2 = 6/5, x4 = 1. Из последней таблицы можно удалить столбцы с искусственными переменными.
Этап 2. Исходная задача примет вид:
Минимизировать: 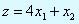
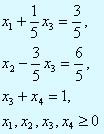
Данной задаче соответствует следующая симплекс-таблица:
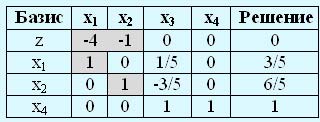
Т.к. базисные переменные x1, x2 имеют ненулевые коэффициенты в z-строке, эту строку следует преобразовать:

Начальная таблица второго этапа примет вид:
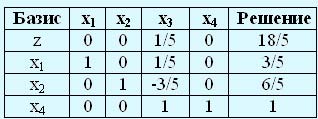
Осталось ввести в базис переменную x3 и применить метод Гаусса-Жордана для расчета строк симплекс-таблицы. В результате будет получено оптимальное решение задачи минимизации. В данной задаче оптимальным решением будет х1 = 2/5, х2 = 9/5, х3 = 1 и z = 17/5.
На следующем шаге рассмотрим применение программы Tora для реализации двухэтапного метода решения задачи линейного программирования.
