На этом шаге мы рассмотрим пример, иллюстрирующий применение первого соотношения.
Рассмотрим прямую и двойственную задачи из примера 1, которые для удобства сведены в следующую таблицу.

В следующей таблице представлены симплекс-итерации решения прямой задачи.
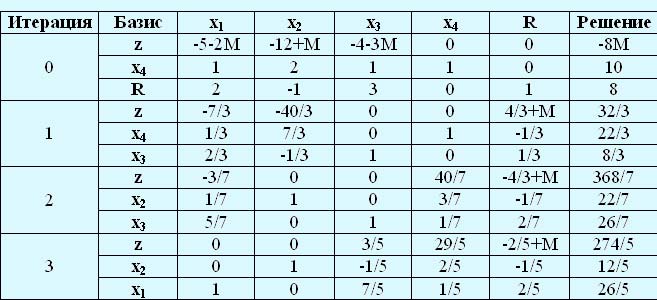
Применяя на третьей симплекс-итерации соотношение 1 для переменных х4 и R из начального базисного решения, получим следующие данные.
Начальные базисные переменные прямой задачи:
1) коэффициенты в z-строке 3-й итерации: x4 = 29/5, R=-2/5+M;
2) соответствующие ограничения двойственной задачи: для x4 – y1 ≥ 0; для R – y2 ≥ -M;
3) уравнения, полученные на основе соотношения 1: для x4 – y1 - 0 = 29/5; для R – y2 – (-M) = -2/5 + М.
Решениями полученных уравнений будут у1 = 29/5 и у2 = - 2/5. Если бы решения двойственной задачи мы искали независимо от решения прямой задачи, то было бы получено такое же решение. Аналогично, вследствие симметричности соотношения 1, из данного решения двойственной задачи и ее начальной симплекс-таблицы получаем оптимальное решение прямой задачи: x1 = 26/5, x2 = 12/5 и х3 = 0.
Применение соотношения 1 к переменным начального решения всегда приводит к легко решаемым уравнениям, так как каждое такое уравнение содержит только одну переменную. Конечно же, ничего не мешает использовать другие переменные (такие, как х1, х2 и х3 в рассматриваемой задаче) при построении уравнений, необходимых для определения значений переменных двойственной задачи. Например, соотношение 1 порождает следующие уравнения, ассоциируемые с переменными х1 и х3.
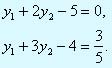
Решение этой системы уравнений также приводит к оптимальным значениям двойственной задачи у1 = 29/5 и у2 = -2/5.
На следующем шаге рассмотрим пример, иллюстрирующий применение второго соотношения.
