На этом шаге мы рассмотрим пример экономической интерпретации ограничений двойственной задачи.
Фабрика игрушек TOYCO собирает три вида игрушек: модели поездов, грузовиков и легковых автомобилей; при сборке каждого вида используется три типа операций. Ежедневный фонд рабочего времени на каждую операцию ограничен предельными величинами 430, 460 и 420 минут. Доход на одну игрушку каждого вида составляет соответственно 3, 2 и 5 д.е. На каждой из трех операций для сборки модели поезда требуется 1, 2 и 1 минуты рабочего времени. Соответствующее время для сборки моделей грузовиков и легковых автомобилей составляет (2,0,4) и (1,2,0) минут (ноль указывает на то, что соответствующая операция не выполняется).
Обозначив через х1, х2 и х3 количество собираемых ежедневно моделей трех видов, получаем прямую и двойственную задачи линейного программирования.
Оптимальное решение предусматривает производство моделей грузовых (х2 = 100) и легковых (х3 = 230) автомобилей и требует отказа от производства моделей поездов (х1 = 0). Это означает, что в текущей экономической ситуации производство моделей поездов не рентабельно.
Вместе с тем рынок игрушек требует выпуска этого вида моделей. Как сделать их производство доходным?
В соответствии с экономической интерпретацией задач линейного программирования, производство моделей поездов будет выгодным только тогда, когда будет выполняться неравенство z1 < с1. Для выполнения этого неравенства нужно либо повысить коэффициент с1 (доход от продажи одной модели поезда), например путем увеличения цены модели, либо снизить стоимость ресурсов z1 (= у1 + 3у2 + у3), необходимых для производства этих игрушек.
Увеличение цены игрушек не желательно, так как это снизит их конкурентоспособность на рынке игрушек.
Уменьшение величины коэффициента z1 более привлекательно, поскольку для этого надо просто сократить время выполнения операций, необходимых для производства моделей поездов.
Обозначим через r1, r2 и r3 величины, пропорциональные долям сокращения времени соответствующих операций. Эти величины находим из условия, чтобы новая стоимость производственных операций не превышала дохода от одной модели поезда. Это условие записывается следующим образом: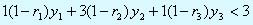 
После подстановки значений y1 = 1, у2 = 2, у3 = 0 получим следующее неравенство:
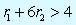
Таким образом, любые значения величин r1 и r2, от 0 до 1, удовлетворяющие неравенству 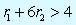, приведут к доходности производства моделей поездов. Например, для значений r1 = 0.6 и r2 = 0.6 получаем z1 – с1 = 4 - 0.6 – 6*0.6 = -0.2.
Вместе с тем отметим, что сокращение времени выполнения второй операции в 6 раз эффективнее сокращения времени выполнения первой операции.
На следующем шаге рассмотрим двойственный симплекс-метод.
