На этом шаге рассмотрим алгоритм двойственного симплекс-метода.
Рассмотрим симплексный алгоритм, который основан на соотношениях между прямой и двойственной задачами. Этот алгоритм эффективно решает определенный класс задач линейного программирования.
В двойственном симплекс-методе решение задачи линейного программирования начинается с недопустимого, но лучшего, чем оптимальное решения. Последовательные итерации этого метода приближают решение к области допустимости без нарушения оптимальности промежуточных решений. Когда будет достигнута область допустимых решений, процесс вычислений заканчивается, так как последнее решение будет оптимальным.
В двойственном симплекс-методе начальная симплекс-таблица обязательно должна иметь в базисном решении недопустимую (т.е. отрицательную) переменную. Для реализации двойственного симплекс-метода разработаны следующие два условия, выполнение которых гарантирует оптимальность последовательных промежуточных решений и приближение их к области допустимых решений.
Двойственное условие допустимости. В качестве исключаемой переменной хr выбирается базисная переменная, имеющая наибольшее по абсолютной величине отрицательное значение. Если таких переменных несколько, то выбор произволен. Если все базисные переменные неотрицательные, процесс вычислений заканчивается.
Двойственное условие оптимальности. Вводимая в базис переменная определяется как переменная, на которой достигается следующий минимум:
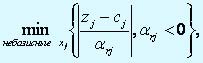
где αrj — коэффициент из симплекс-таблицы, расположенный на пересечении ведущей строки (соответствующей исключаемой переменной хr) и столбца, соответствующего переменной xj. При наличии нескольких альтернативных переменных, выбор делается произвольно.
На следующем шаге рассмотрим пример решения задачи с помощью двойственного симплекс-метода.
