На этом шаге рассмотрим применение двойственного симплекс-метода для решения задачи линейного программирования.
Дана задача линейного программирования:
Минимизировать 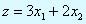
При ограничениях 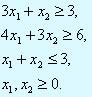
Начальная симплекс-таблица имеет вид:
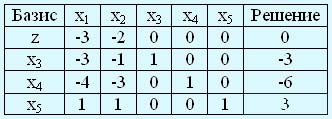
Среди дополнительных переменных этой задачи х3 и х4 являются избыточными, а x5 — остаточной. Умножим каждое равенство, соответствующее избыточным дополнительным переменным, на -1; в результате правые части этих равенств непосредственно указывают на базисные переменные, которые являются недопустимыми (х3 = -3, х4 = -6, х5 = 3). Этот подход всегда используется при реализации двойственного симплекс-метода.
Поскольку zj – сj ≤ 0 для всех j = 1,..., 5, начальное базисное решение является оптимальным (но не допустимым). Таким образом, приведенная таблица удовлетворяет требованиям начальной таблицы двойственного симплекс-метода, а именно — оптимальности и недопустимости.
Двойственное условие допустимости указывает на переменную х4 (= -6) как на вводимую в базис. Теперь применим двойственное условие оптимальности для определения исключаемой переменной. Для этого используем следующую таблицу.
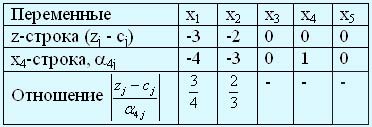
Приведенные отношения показывают, что исключаемой переменной будет х2. Отметим, что переменные хj будут кандидатами на исключение из базисного решения только тогда, когда коэффициент α4j будет строго отрицательным. По этому критерию переменные x3, х4, х5 не рассматриваются как кандидаты на исключение из базиса.
Следующая таблица получена с помощью известных операций над строками, применяемых в прямом симплекс-методе.

Последняя таблица показывает, что из базиса исключается переменная x3 и вводится x1. В результате получаем следующую симплекс-таблицу.
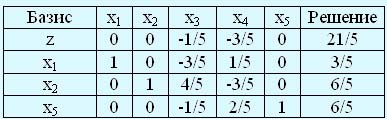
Решение, представленное в последней таблице, допустимо (и оптимально), поэтому вычисления заканчиваются. Это решение имеет вид х1 = 3/5, х2 = 6/5, z = 21/5.
На рис. 1 показана последовательность шагов двойственного симплекс-метода при решении этой задачи.
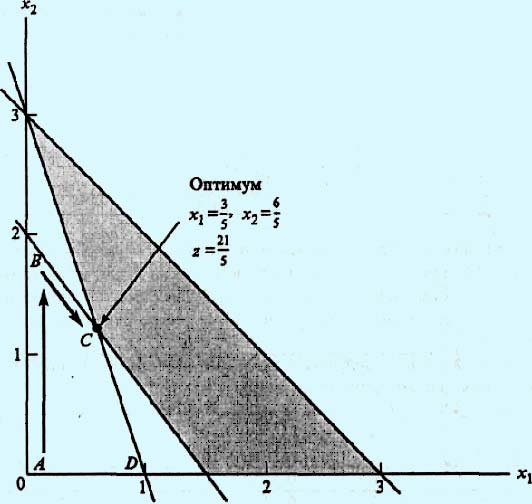
Рис. 1. Последовательность шагов двойственного симплекс-метода
Алгоритм начинается в крайней точке А (которой соответствует недопустимое, но "лучше, чем оптимальное" решение), затем он переходит к точке В (которой также соответствует недопустимое, но "лучше, чем оптимальное" решение) и заканчивается в точке С, уже принадлежащей области допустимых решений.
На следующем шаге мы приведем несколько задач.
