На этом шаге мы остановимся на тех данных, которые будем использовать в дальейшем для анализа.
Для иллюстрации различных алгоритмов мы будем использовать несколько наборов данных. Некоторые наборы данных будет небольшими и синтетическими (то есть выдуманными), призванными подчеркнуть отдельные аспекты алгоритмов. Другие наборы данных будут большими, реальными примерами.
Примером синтетического набора данных для двухклассовой классификации является набор данных forge, который содержит два признака. Программный код, приведенный ниже, создает диаграмму рассеяния (рисунок 1), визуализируя все точки данных в этом наборе.
[In 6]: import mglearn import matplotlib.pyplot as plt # генерируем набор данных X, y = mglearn.datasets.make_forge() # строим график для набора данных %matplotlib inline mglearn.discrete_scatter(X[:, 0], X[:, 1], y) plt.legend(["Класс 0", "Класс 1"], loc=4) plt.xlabel("Первый признак") plt.ylabel("Второй признак") print("форма массива X: {}".format(X.shape))
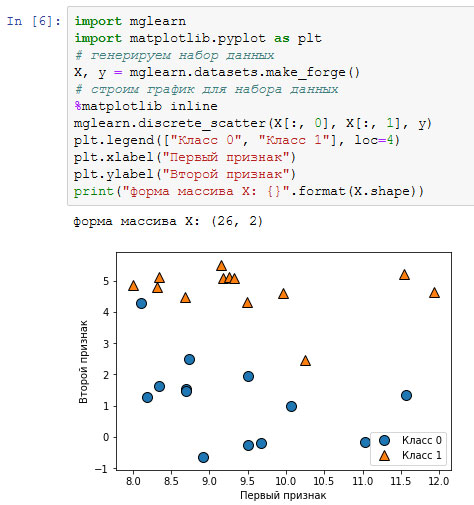
Рис.1. Диаграмма рассеяния для набора данных forge
На графике первый признак отложен на оси х, а второй - по оси у. Как это всегда бывает в диаграммах рассяения, каждая точка данных представлена в виде одного маркера. Цвет и форма маркера указывает на класс, к которому принадлежит точка (рисунок 1).
Как видно из сводки по массиву X, этот набор состоит из 26 точек данных и 2 признаков. Для иллюстрации алгоритмов регрессии, мы воспользуемся синтетическим набором wave. Набор данных имеет единственный входной признак и непрерывную целевую переменную или отклик (response), который мы хотим смоделировать. На рисунке, построенном здесь (рисунок 2), по оси x располагается единственный признак, а по оси у - целевая переменная (ответ).
[In 7]: X, y = mglearn.datasets.make_wave(n_samples=40) plt.plot(X, y, 'o') plt.ylim(-3, 3) plt.xlabel("Признак") plt.ylabel("Целевая переменная")
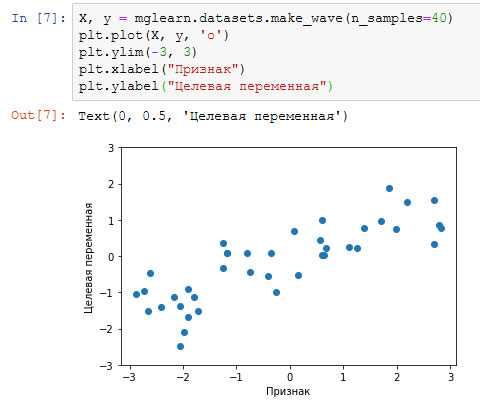
Рис.2. График для набора данных wave, по оси x отложен признак, по оси у - целевая переменная
Мы используем эти очень простые, низкоразмерные наборы данных, потому что их легко визуализировать - печатная страница имеет два измерения, и данные, которые содержат более двух признаков, графически представить трудно. Вывод, полученный для набора с небольшим числом признаков или низкоразмерном (low-dimensional) наборе, возможно, не подтвердится для набора данных с большим количеством признаков или высокоразмерного (high-dimensional) набора. Если вы помните об этом, проверка алгоритма на низкоразмерном наборе данных может оказаться очень полезной.
Мы дополним эти небольшие синтетические наборы данных двумя реальными наборами, которые включены в scikit-learn. Один из них - набор данных по раку молочной железы Университета Висконсин (cancer для краткости), в котором записаны клинические измерения опухолей молочной железы. Каждая опухоль обозначается как "benign" ("доброкачественная", для неагрессивных опухолей) или "malignant" ("злокачественная", для раковых опухолей), и задача состоит в том, чтобы на основании измерений ткани дать прогноз, является ли опухоль злокачественной.
Данные можно загрузить из scikit-learn с помощью функции load_breast_cancer:
[In 10]: from sklearn.datasets import load_breast_cancer cancer = load_breast_cancer() print("Ключи cancer(): \n{}". format(cancer.keys())) Ключи cancer(): dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename'])
Наборы данных, которые включены в scikit-learn, обычно хранятся в виде объектов Bunch, которые содержат некоторую информацию о наборе данных, а также фактические данные.
Все, что вам нужно знать об объектах Bunch - это то, что они похожи на словари, с тем преимуществом, что вы можете прочитать значения, используя точку (bunch.key вместо bunch['key']).
Набор данных включает 569 точек данных и 30 признаков.
[In 12]: print("Форма массива data для набора cancer: {}".format(cancer.data.shape)) Форма массива data для набора cancer: (569, 30)
Из 569 точек данных 212 помечены как злокачественные, а 357 как доброкачественные.
[In 15]: import numpy as np print("Количество примеров для каждого класса:\n{}".format( {n: v for n, v in zip(cancer.target_names, np.bincount(cancer.target))})) Количество примеров для каждого класса: {'malignant': 212, 'benign': 357}
Чтобы получить содержательное описание каждого признака, взглянем на атрибут feature_names:
[In 17]: print("Имена признаков:\n{}".format(cancer.feature_names)) Имена признаков: ['mean radius' 'mean texture' 'mean perimeter' 'mean area' 'mean smoothness' 'mean compactness' 'mean concavity' 'mean concave points' 'mean symmetry' 'mean fractal dimension' 'radius error' 'texture error' 'perimeter error' 'area error' 'smoothness error' 'compactness error' 'concavity error' 'concave points error' 'symmetry error' 'fractal dimension error' 'worst radius' 'worst texture' 'worst perimeter' 'worst area' 'worst smoothness' 'worst compactness' 'worst concavity' 'worst concave points' 'worst symmetry' 'worst fractal dimension']
Если вам интересно, то более подробную информацию о данных можно получить, прочитав cancer.DESCR.
Кроме того, для задач регрессии мы будем использовать реальный набор данных - набор данных Boston Housing. Задача, связанная с этим набором данных, заключается в том, чтобы спрогнозировать медианную стоимость домов в нескольких районах Бостона в 1970-е годы на основе такой информации, как уровень преступности, близость к Charles River, удаленность от радиальных магистралей и т.д. Набор данных содержит 506 точек данных и 13 признаков:
[In 20]: from sklearn.datasets import load_boston boston = load_boston() print("Фopмa массива data для набора boston: {}".format(boston.data.shape)) Фopмa массива data для набора boston: (506, 13)
Опять же, вы можете получить более подробную информацию о наборе данных, прочитав атрибут boston.DESCR. В данном случае мы более детально проанализируем набор данных, учтя не только 13 измерений в качестве входных признаков, но и приняв во внимание все взаимодействия (interactions) между признаками. Иными словами, мы будем учитывать в качестве признаков не только уровень преступности и удаленность от радиальных магистралей по отдельности, но и взаимодействие уровень преступности-удаленность от радиальных магистралей. Включение производных признаков называется конструированием признаков (feature engineering), которое мы рассмотрим более подробно позже4. Набор данных c производными признаками можно загрузить с помощью функции load_extended_boston:
[In 21]: X, y = mglearn.datasets.load_extended_boston() print("Форма массива X: {}".format(X.shape)) Форма массива X: (506, 104)
Полученные 104 признака - 13 исходных признаков плюс 91 производный признак.
Мы будем использовать эти наборы данных, чтобы объяснить и проиллюстрировать свойства различных алгоритмов машинного обучения. Однако сейчас давайте перейдем к самим алгоритмам. Сейчас мы вернемся к алгоритму к ближайших соседей, который рассматривали на 21 шаге.
Архив блокнота со всеми приведенными на этом шаге вычислениями можно взять здесь.
На следующем шаге мы рассмотрим метод k ближайших соседей.
