На этом шаге мы рассмотрим использование этого алгоритма.

    Алгоритм k ближайших соседей, возможно, является самым простым алгоритмом машинного обучения. Построение модели заключается в запоминании обучающего набора данных. Для того, чтобы сделать прогноз для новой точки данных, алгоритм находит ближайшие к ней точки обучающего набора, то есть находит "ближайших соседей".

Классификация с помошью k соседей

    В простейшем варианте алгоритм k ближайших соседей рассматривает лишь одного ближайшего соседа - точку обучающего набора, ближе всего расположенную к точке, для которой мы хотим получить прогноз. Прогнозом является ответ, уже известный для данной точки обучающего набора. На рисунке 1 показано решение задачи классификации для набора данных forge:

[In 4]:
import mglearn
mglearn.plots.plot_knn_classification(n_neighbors=1)

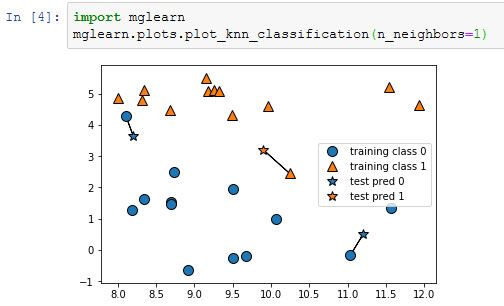
Рис.1. Прогнозы, полученные для набора данных forge с помощью модели одного ближайшего соседа

    Здесь мы добавили три новые точки данных, показанные в виде звездочек. Для каждой мы отметили ближайшую точку обучающего набора. Прогноз, который дает алгоритм одного ближайшего соседа - метка этой точки (показана цветом маркера).

    Вместо того, чтобы учитывать лишь одного ближайшего соседа, мы можем рассмотреть произвольное количество (k) соседей. Отсюда и происходит название алгоритма k ближайших соседей. Когда мы рассматриваем более одного соседа, для присвоения метки используется голосование (voting). Это означает, что для каждой точки тестового набора мы подсчитываем количество соседей, относящихся к классу 0, и количество соседей, относящихся к классу 1. Затем мы присваиваем точке тестового набора наиболее часто встречающийся класс: другими словами, мы выбираем класс, набравший большинство среди k ближайших соседей. В примере, приведенном ниже (рисунок 2), используются три ближайших соседа:

[In 5]:
mglearn.plots.plot_knn_classification(n_neighbors=3)

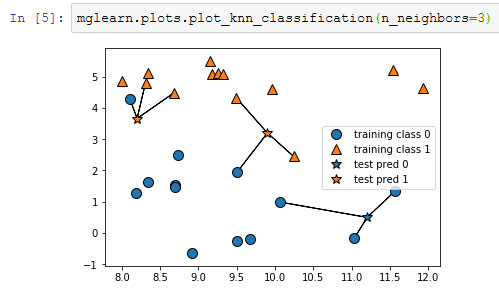
Рис.1. Прогнозы, полученные для набора данных forge с помощью модели трех ближайших соседей

    И снова прогнозы переданы цветом маркера. Видно, что прогноз для новой точки данных в верхнем левом углу отличается от прогноза, полученного при использовании одного ближайшего соседа.

    Хотя данный рисунок иллюстрирует задачу бинарной классификации, этот метод можно применить к наборам данных с любым количеством классов. В случае мультиклассовой классификации мы подсчитываем количество соседей, принадлежащих к каждому классу, и снова прогнозируем наиболее часто встречающийся класс.

    Теперь давайте посмотрим, как можно применить алгоритм к ближайших соседей, используя scikit-learn. Во-первых, мы разделим наши данные на обучающий и тестовый наборы, чтобы оценить обобщающую способность модели, рассмотренную на на 19 шаге:

[In 8]:
from sklearn.model_selection import train_test_split 
X, y = mglearn.datasets.make_forge()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

    Далее выполняем импорт и создаем объект-экземпляр класса, задавая параметры, например, количество соседей, которое будем использовать для классификации. В данном случае мы устанавливаем его равным 3:

[In 9]:
from sklearn.neighbors import KNeighborsClassifier 
clf = KNeighborsClassifier(n_neighbors=3)

    Затем подгоняем классификатор, используя обучающий набор. Для KNeighborsClassifier это означает запоминание набора данных, таким образом, мы можем вычислить соседей в ходе прогнозирования:

[In 10]:
clf.fit(X_train, y_train)

[Out 10]:
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
           metric_params=None, n_jobs=None, n_neighbors=3, p=2,
           weights='uniform')

    Чтобы получить прогнозы для тестовых данных, мы вызываем метод predict. Для каждой точки тестового набора он вычисляет ее ближайших соседей в обучающем наборе и находит среди них наиболее часто встречающийся класс:

[In 11]:
print("Прогнозы на тестовом наборе: {}".format(clf.predict(X_test)))

Прогнозы на тестовом наборе: [1 0 1 0 1 0 0]

    Для оценки обобщающей способности модели мы вызываем метод score с тестовыми данными и тестовыми метками:

[In 12]:
print("Правильность на тестовом наборе: {:.2f}".format(clf.score(X_test, y_test)))

Правильность на тестовом наборе: 0.86

    Мы видим, что наша модель имеет правильность 86%, то есть модель правильно предсказала класс для 86% примеров тестового набора.

    На следующем шаге мы рассмотрим анализ KNeighborsClassifier.

Предыдущий шаг Содержание Следующий шаг